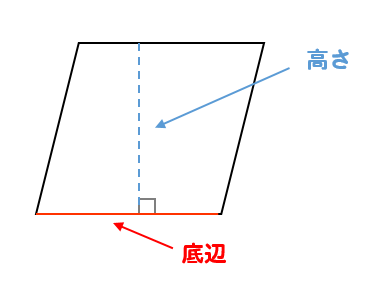
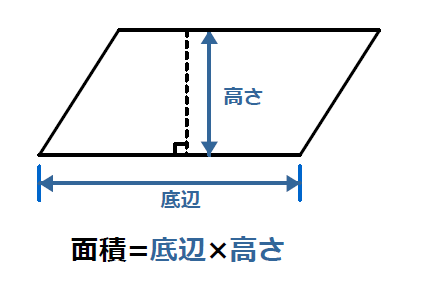
1 平行四辺形の高さを選ぶ。 〇 平行四辺形の高さは、図形の外に位置付くことがある ことを捉えること 2 底辺も高さも等しい場合の面積を調べる。 〇 どのような平行四辺形でも底辺と高さが等しい場合、 面積も等しくなることを捉えること 平行四辺形の面積(公式・証明) 平行四辺形の面積の求め方についてです。 平行四辺形の面積は、 「底辺×高さ」 で求めることができます。 証明はとても簡単です。平行四辺形を面積を変えずに長方形の形にするという方法です。平行四辺形の面積を求めるにはどうしたらいいでしょうか。 台形を2つ合わせて,あるいは三角形と台形を合わせて長方形にしてみると公式が使えます。 つまり,平行四辺形の面積は 底辺×高さ で求めら
平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典
平行四辺形 面積 求め方 公式
平行四辺形 面積 求め方 公式-平行四辺形 面積計算 公式 求め方 高さ 底辺 自動 面積 平行四辺形 面積; 底辺に垂直なところが高さになるのは後ほど解説します。 つまり、この平行四辺形では、高さは底辺に垂直な 5cm 5 c m のところとなります。 平行四辺形の面積は、 8×5=40 8 × 5 = 40 となります。 よって、この平行四辺形の面積は 40cm2 40 c m 2 となります。
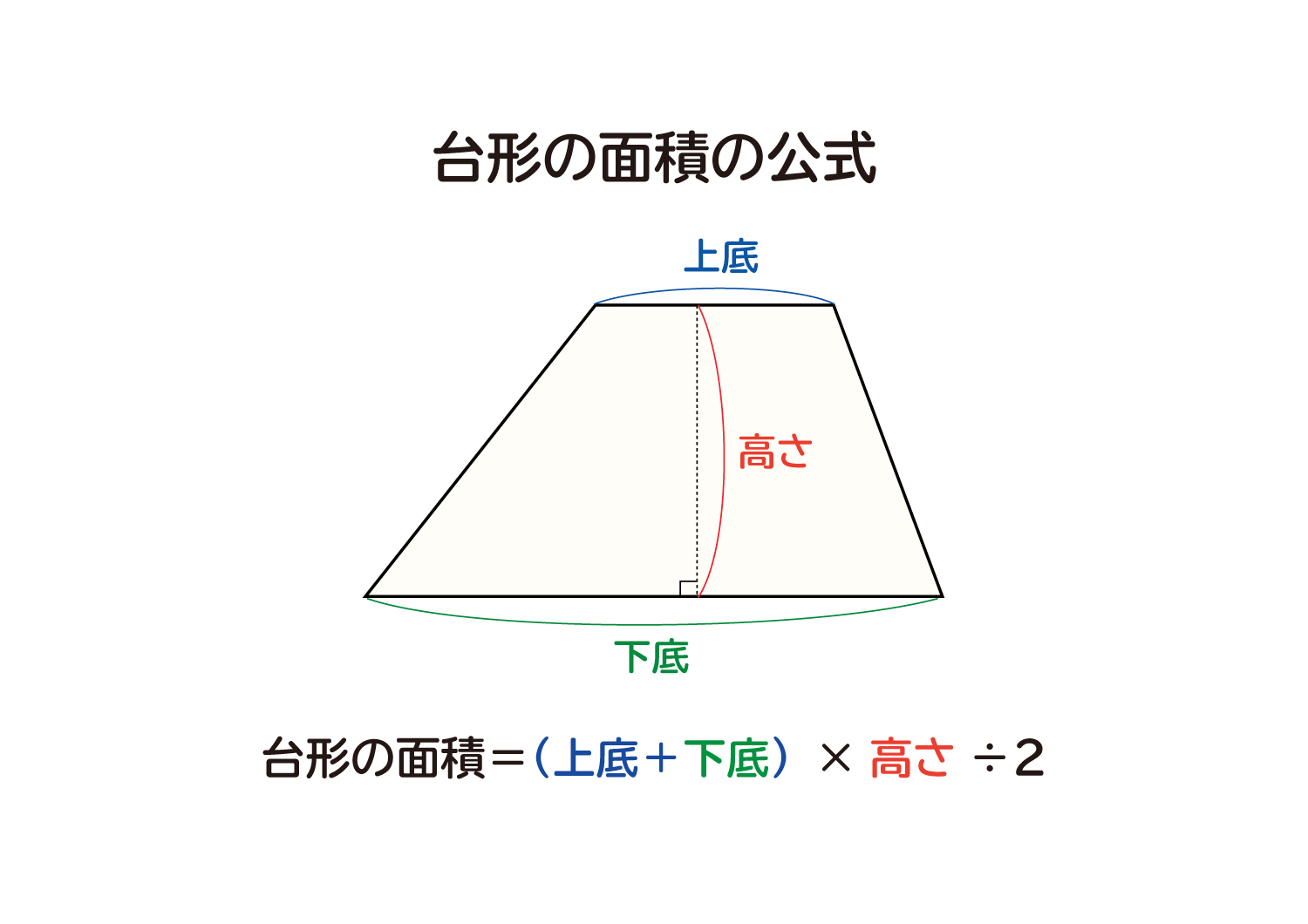



なぜ 台形の面積は 上底 下底 高さ 2 なのか を説明します おかわりドリル
中学数学 図形 平行四辺形とは? 定義・条件・性質や面積の公式、証明問題 21年2月19日 この記事では、「平行四辺形」の定義や条件、性質をできるだけわかりやすく解説していきます。 また、平行四辺形の面積の公式や、対角線の角度などの計算問題面積の公式をつくり 出し、 平行四辺形の面積を 求めることができる。 求めることができる。 4 平行四辺形の面積を 工夫して求めること ができる。 子どもたちの考え方から高さが何 ・対角線で分けて移動する。 ・平行四辺形を二つに分割して考える。 2平行四辺形の面積 A: B: 面積: 円 円 半円 扇形 円周長から面積 四角形 四角形 四角形 4辺と対角線 角パイプ 三角形 三角形 三角形(3辺) 四角形 平行四辺形 ひし形 台形 LC形 L形 C形 円形
② 求積公式を基にして,三角形や平行四辺形などの面積を求めること (2)本単元の目標 関心・意欲・態度 数学的な考え方 技能 知識・理解 既習の面積公式を基に, 三角形や平行四辺形などの 面積を求める公式を進んで 見いだそうとしている。平行四辺形の面積を求める公式に代入して、計算するだけですね。 平行四辺形の面積 = 底辺 ×高さ = 6× 5 = 30cm2 平行四辺形の面積 = 底辺 × 高さ = 6 × 5 = 30 cm 2三角形の面積(3辺からヘロンの公式) 三角形の面積(1辺と2角から) 正方形の面積 長方形の面積 台形の面積 台形の高さ・面積(4辺の長さから) 台形の1辺・面積(3辺の長さと高さから) ひし形の面積 平行四辺形の面積(底辺と高さから)
「ア 三角形や平行四辺形、ひし形及び台形の面積の 求め方」には、「三角形や平行四辺形、及び台形の面 積の求め方を、既習の求積可能な図形の面積の求め方 を基に考えたり、説明したり、公式を作り台形の面積を求める公式は 台形の面積 上底 下底 高さ 台 形 の 面 積 = ( 上 底 下 底) × 高 さ ÷ 2 なので、 台形の面積 台 形 の 面 積 = ( 5 7) × 4 ÷ 2 = 12 × 4 ÷ 2 = 24 ( c m 2) になります。 次は小数点を含む台形の面積を計算します。 今回は、平行四辺形の面積の求め方について書いていきたいと思います。 平行四辺形の面積を求める公式 平行四辺形の面積を求める問題 問題① 《平行四辺形の面積の求め方》 問題② 《平行四辺形の面積の求め方》 問題③ 《平行四辺形の高さの求め方》 問題④ 《平行四辺形の底辺の求め方



平行四辺形とひし形の違いってなに それぞれの特徴を比較 数スタ




File 平行四辺形の面積 1 Png Wikimedia Commons
・平行四辺形の面積公式と適用 1 ・高さが平行四辺形の外にあるときでも公式が適用でき ること 2 三角形の面積の求め ② ・三角形の面積の求め方 方 ・三角形の底辺,高さの意味 ・三角形の面積公式と適用 1 ・高さが三角形の外にあるときでも面積公式が適用でき ること 3 いろいろ長方形の面積 平行四辺形の面積 三角形の面積 台形の面積 円の面積 算数では様々な公式を覚えます。 しかしその公式の意味を知っている方は多くないと思います。 本ホームページでは公式の意味や公式の導き方を図を使用して分かりやすく説明して平行四辺形の面積の求め方を考 える。 ・ 平行四辺形の面積の求め方を、 長方形に等積変形して説明する。 児童が説明する算数的活動① 平行四辺形を 求積できる図 形に変形し、進 んで平行四辺 形の面積を求 めようとして いる。(ア、イ) 平行四辺形の
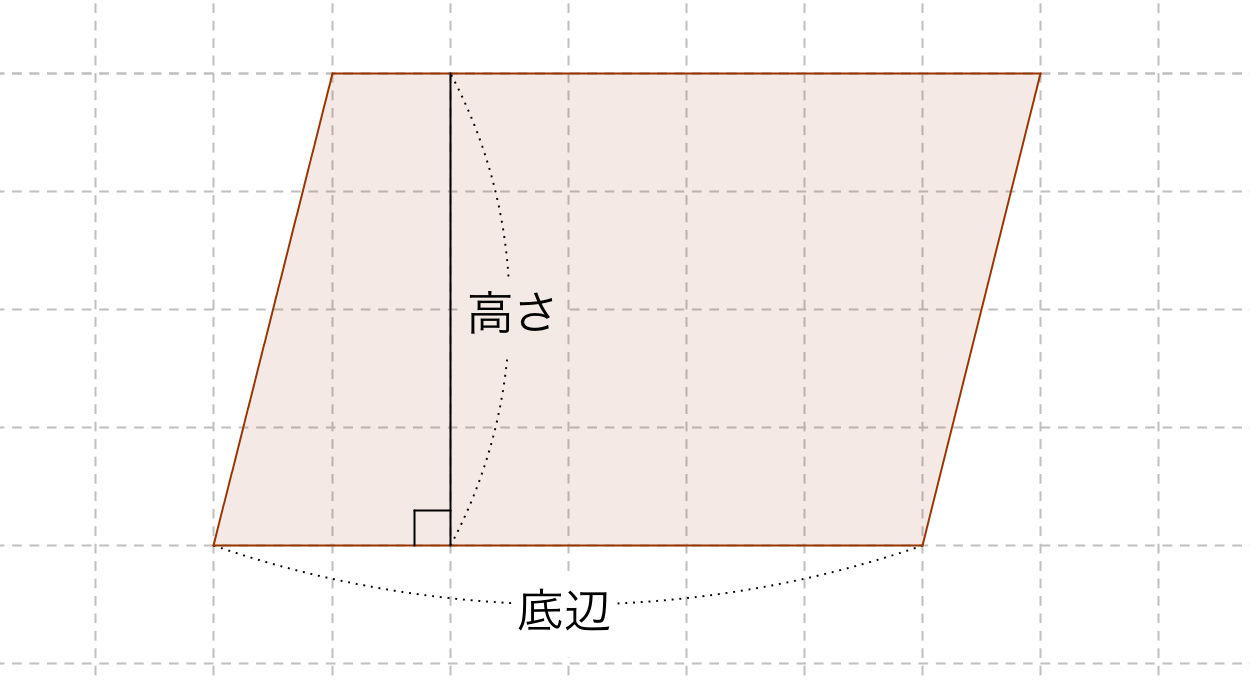



平行四辺形の面積の公式 算数の公式




簡単公式 ひし形 菱形 の面積を計算できる2つの求め方 Qikeru 学びを楽しくわかりやすく
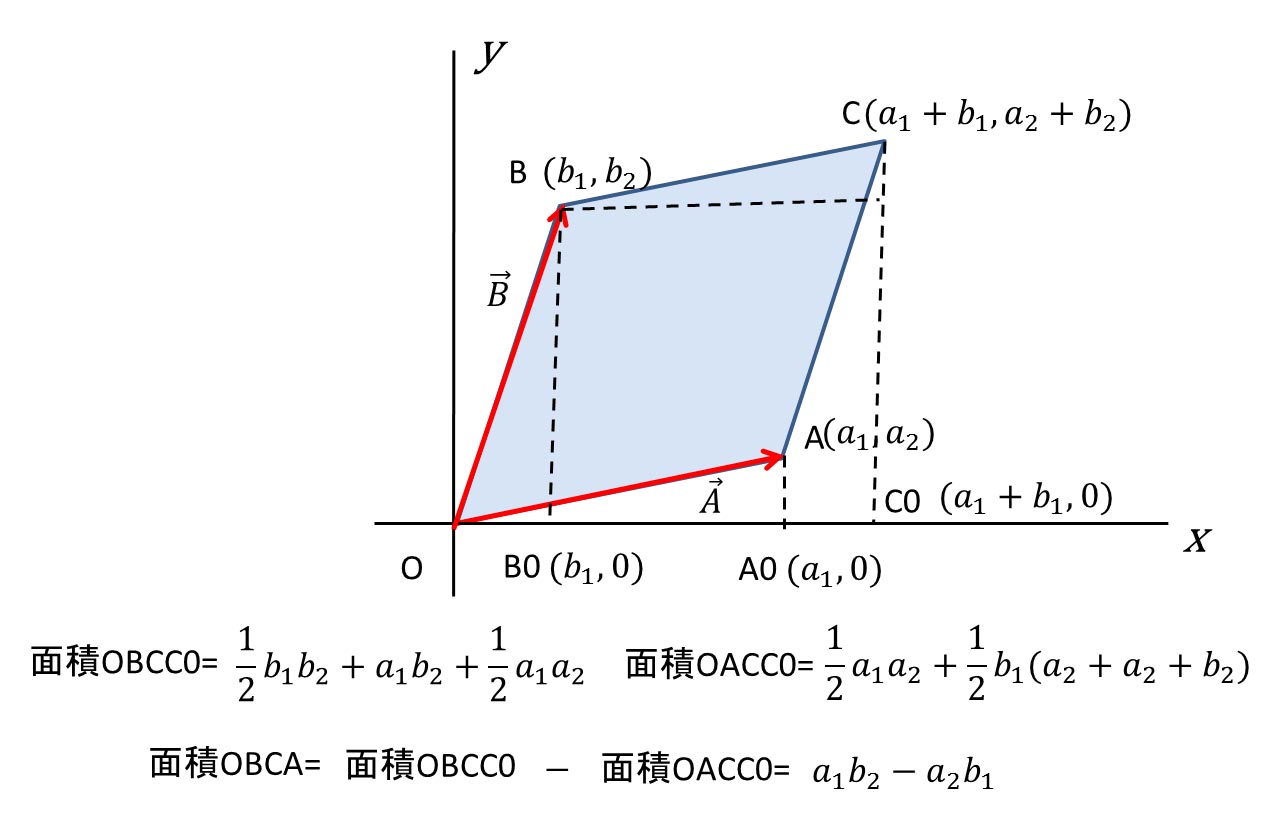
平行四辺形の面積をくふうして求めよう 4 積 知平行四辺形の面積の公式を 理解する。 3 い ろ い ろ な 三 角 形 ・ 四 角 形 の 面 積 6 / 12 ・教科書の付録を使って高さが外にあ る三角形を三角形や平行四辺形に変 形させ,面積を求める公式が適用で きることを理解する。 ・作業的な活動平行四辺形の面積の求め方 平行四辺形の求積公式 平行四辺形の求積 公式の適用 既習の長方形に変形することで、平行四辺形の面積が求 められることを説明する。 既習の面積の求め方をもとに、図形の構成要素として直 角に着目し、長方形と平行四辺形の以上で二つのベクトルが作る平行四辺形の面積は、それらのベクトル積の大きさに等しいことがわかりました。 ベクトル \(\overrightarrow{a} = \langle2, 0, 0 \rangle\) と \(\overrightarrow{b} = \langle 1, 1, 0 \rangle\) が作る平行四辺形の面積を求めよ。



5年算数面積2 教え方のポイント
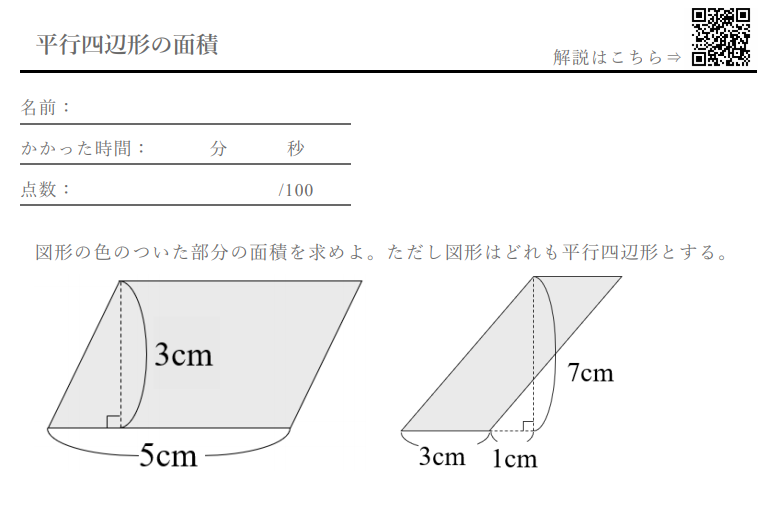



平行四辺形 の面積 計算ドリル 問題集 数学fun
公式集:ベクトル G ベクトルと a =(a1,a2), b =(b1,b2)が作る平行四辺形の面積S はS = a1b2 −a2b1 である。 G27 直線のベクトル方程式 直線l が2点A, B を通るとき,2点A, B の位置ベクトルをa = −→ OA, b = −−→ OBと し,v = −−→ AB = b −a とする。直線l 上の任意の点P の位置ベクトルひし形の面積の公式 ひし形の面積は 2 2 つの対角線の長さをかけて2で割ったもの、つまり 『対角線×対角線÷2 ÷ 2 』 で求めることができます。公式を使わない平行四辺形の面積問題! 算数パズル10秒で解けますか? 公式を使わない平行四辺形の面積問題! If playback doesn't




平行四辺形の面積 ベクトルでの公式 理数系無料オンライン学習 Kori
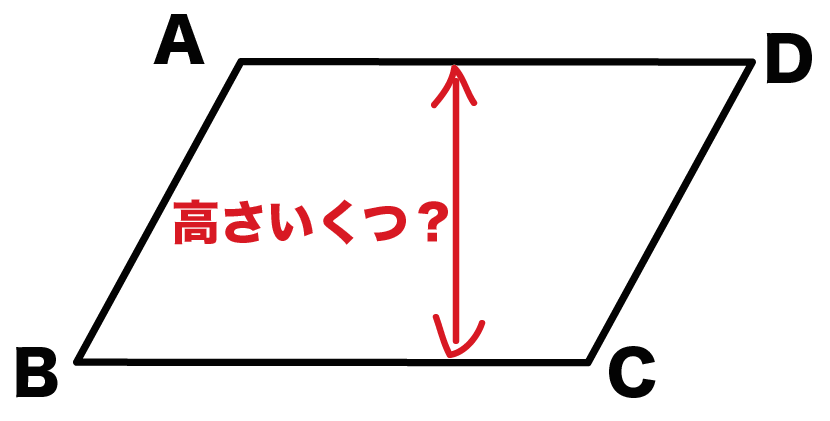



中学数学 平行四辺形の高さの2つの求め方 Qikeru 学びを楽しくわかりやすく
平行四辺形の面積の公式 平行四辺形の面積は 『底辺×高さ』 で求めることができます。 たとえば以下のような問題の場合。5年 台形の面積|算数イメージ動画集|大日本図書 文部科学省『教育用コンテンツ開発事業』 台形の面積を求めるにはどうしたらいいでしょうか。 すでに学習した平行四辺形の面積の公式を使ってみましょう。 同じ面積の台形を2つ合わせて平行四辺形・ 平行四辺形の面積=底辺×高さ ・ 台形の面積=(上底+下底)×高さ÷2 ・ ひし形の面積=対角線×対角線÷2 面積の公式 ⑴ 三角形 ⑵ 平行四辺形 高さが三角形や平行四辺形の外にある図形でも,公式をつかって,図形の面



子どもを混乱させる相似な三角形の2つの面積比 算数数学が苦手な子専門のプロ家庭教師みかん先生



エクセルのグラフで学ぶ気象学 補説05
平行四辺形の面積を求めるときは、 (底辺) × (高さ) の公式から導く のではなく、 上記のような三角形を移動する考え方を頭の中でするけど、解答用紙に全部書くのめんどくさいから、 結論の (底辺) × (高さ) だけ をを書くっていう、思考回路です。裏ワザ公式は、答えがあっているかの確認などで 利用してもらえれば効果バツグンなはずです(^^) 相似平行四辺形と面積比の問題を徹底解説! 相似な図形 中3数学相似な図形の見つけ方、相似条件とは?基本問題を使って解説! 相似な図形 相似の利用木の高さ平行四辺形の面積の求め方を理解したら、 平行四辺形の面積を求める公式を整理させてください。 公式の理解ができたら、公式を覚える練習をさせましょう。 公式 平行四辺形の面積=底辺×高さ (ていへん かける たかさ) 教え方2三角形の面積の求め方 三角形の面積の求め方を考えさせます




なぜ 台形の面積は 上底 下底 高さ 2 なのか を説明します おかわりドリル




平行四辺形の面積の求め方教えてください Clear
ベクトルの平行四辺形の面積公式 三角形OABの面積をベクトルを用いて表せたら、平行四辺形OACBの面積も簡単に導出できます。 平行四辺形の対角線を引くと、合同な三角形が 2 つ重なっている形となっています。 平行四辺形の面積は、 「面積 底辺 高さ」 「 面 積 = 底 辺 × 高 さ 」 で求められます。 たとえば、「底辺 4 c m ,高さ 3 c m の平行四辺形」の面積は 4 × 3 = 12 c m 2 となります。 これは、平行四辺形の右端の直角三角形を切り取って左側に移すと 「たて 3 c mア 三角形、平行四辺形、ひし形及び台形の面積の求め方を考えること。 本単元では、等積変形や倍積変形を利用して、平行四辺形や三角形などの面積を多様な考え方で求め る活動を位置付ける。その活動を通して、既習の求積公式が利用できる図形に変形
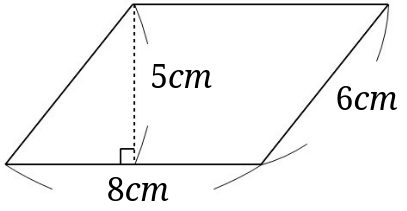



平行四辺形の面積の求め方で習う公式は なぜ底辺 高さになるの みけねこ小学校




平行四辺形の面積の求め方 公式と計算例
平行四辺形の面積を求める活動では「三角形の面積を基にする考え方 「長方形の面積を基,」, にする考え方」の2つの考えが出ると思われる。それゆえ,前時で同じ方法の見通しをもった者 同士で意見交換する場を設ける。 本時では,2つのコースの考え方を説明し合う活動をとり,それぞれ台形の面積の公式を「よむ」5年生 右のように台形を 2つ組み合わせると平行四辺形ができます平行四辺 形の面積=底辺×高さで底辺のところが台形の上底+下底になってい ますだから台形の面積=(上底+下底)×高さ÷2です面積の公式、数値入力による面積の計算。公式のたしかめや計算の確かめに利用できます。 top情報室へ 半角の数字をお使いください。by sakata 正方形の面積 正方形の面積の求め方の公式? 正方形の面積を求めます。一辺を、入力してください。 正方形の面積は次のとおりです。 平行四辺形




小5 算数 小5 41 平行四辺形の面積 Youtube




勉強しよう数学 2重平行四辺形の面積の公式
三角形 (さんかくけい) の 面積 (めんせき) の求め方の 基本 (きほん) は「 底辺 (ていへん) × 高 (たか) さ ÷ 2」ですが、高さが分からないときに 他 (た) の 情報 (じょうほう) から面積を求める 公式 (こうしき) がいくつもあります。 ここでは、三辺の長さが分かっている 場合 (ばあい) や、 角度




File 平行四辺形の面積1 Png Wikimedia Commons




高校数学b ベクトルの成分表示と平行四辺形 受験の月




高校数学 平行四辺形の面積の求め方 練習編 映像授業のtry It トライイット




平行四辺形の対角線の長さの求め方
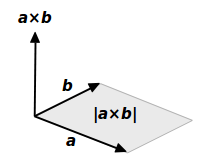



ベクトル積の大きさは平行四辺形の面積 ベクトル解析 基礎からの数学入門
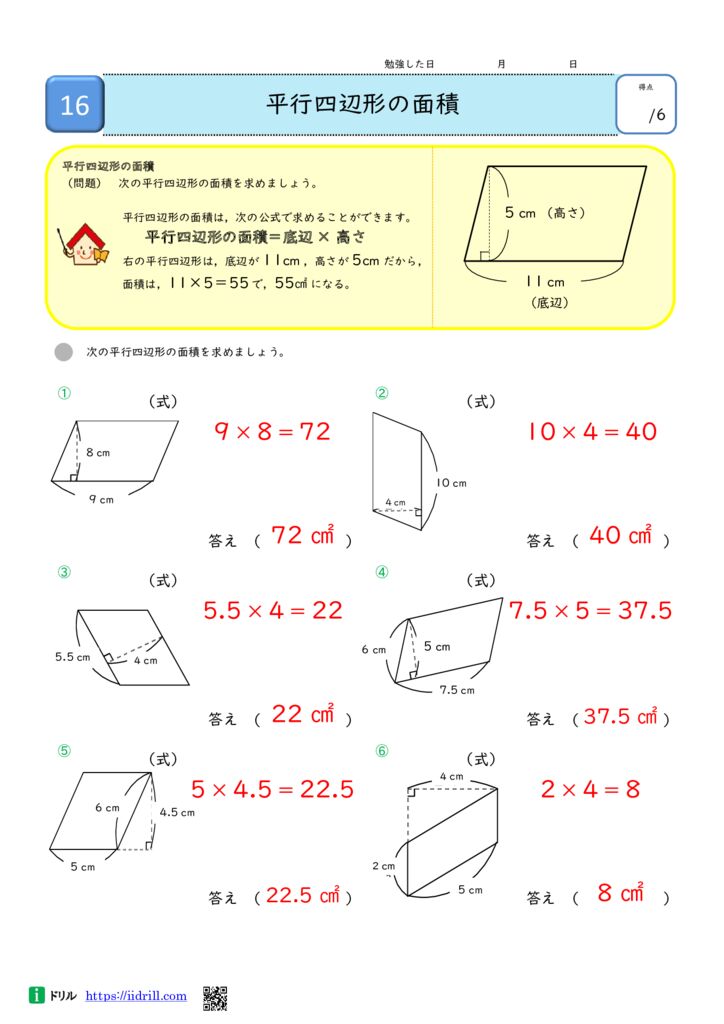



5年生算数ドリル 面積




公式なんて覚えない ひし形の面積は直感的に考えよう




ひし形の面積の公式 面積の求め方は対角線に注目しよう 中学や高校の数学の計算問題
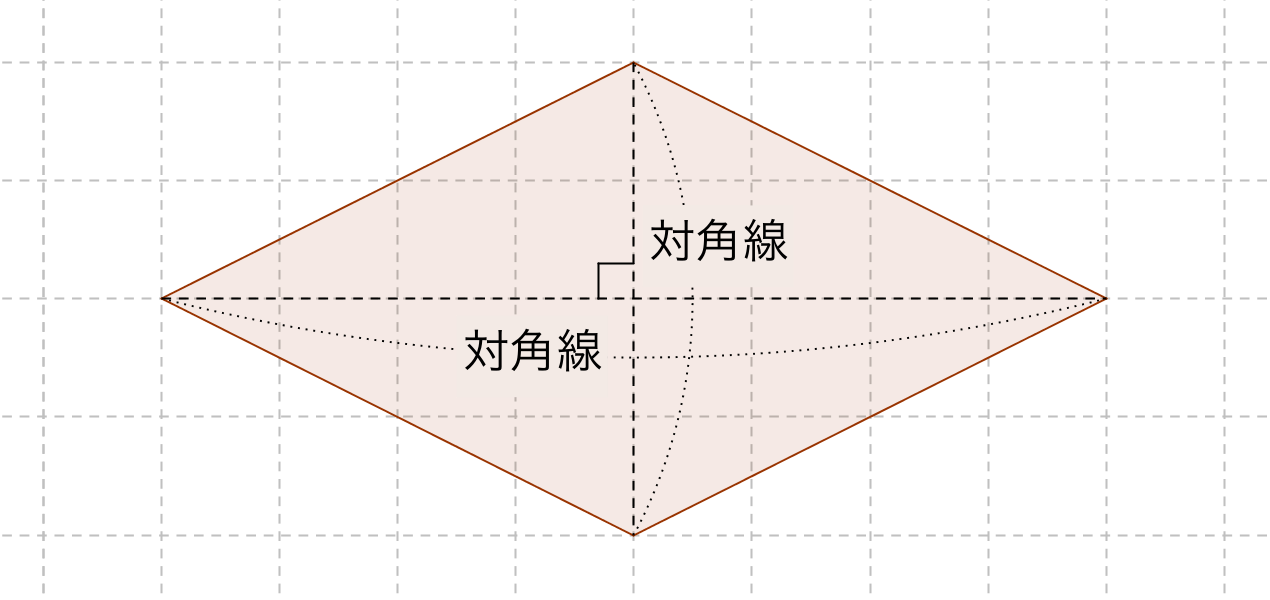



ひし形の面積の公式 算数の公式
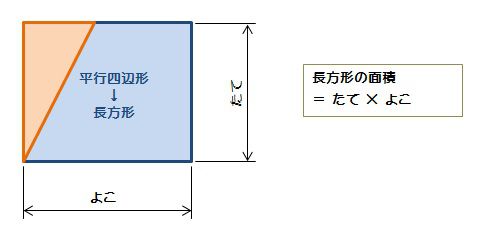



平行四辺形の面積 算数の公式覚えてますか




平行四辺形の面積の求め方 公式と計算例




平行四辺形の面積の求め方 公式と計算例




2次の正方行列式と平行四辺形の面積 機械学習に詳しくなりたいブログ



面積5 12の流れ




面積 平行四辺形の面積 01 平行四辺形の面積の公式 Youtube



1



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典
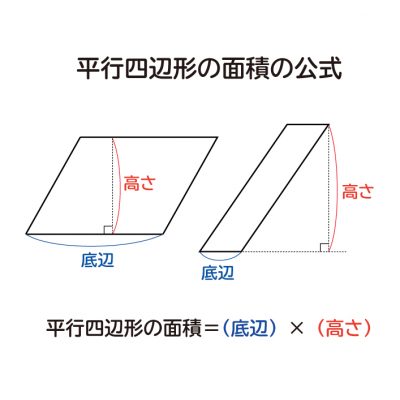



なぜ 台形の面積は 上底 下底 高さ 2 なのか を説明します おかわりドリル




面積6 12の流れ
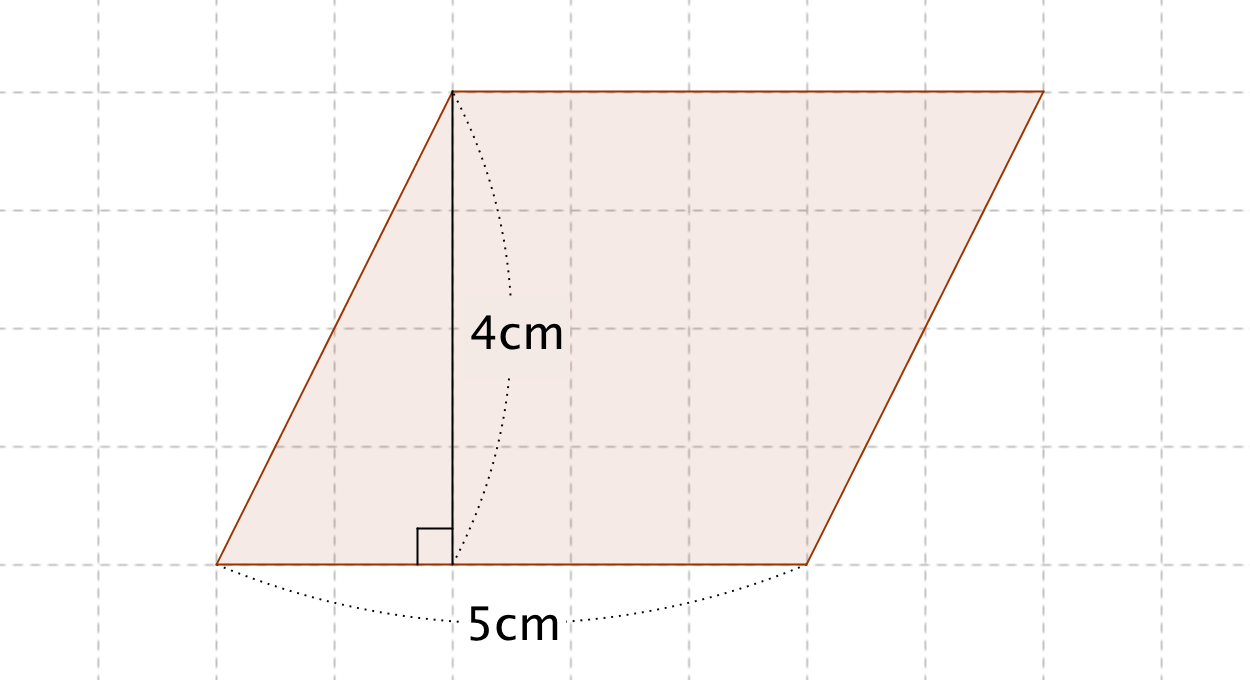



平行四辺形の面積の公式 算数の公式
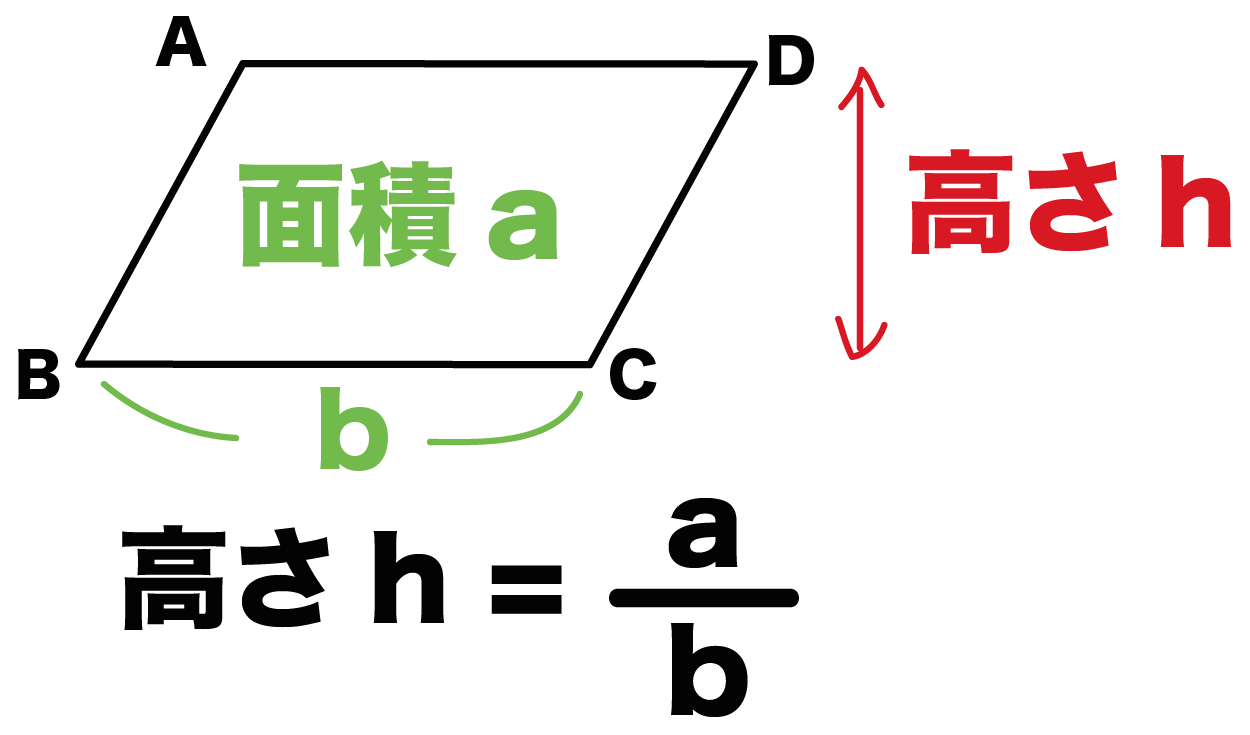



中学数学 平行四辺形の高さの2つの求め方 Qikeru 学びを楽しくわかりやすく
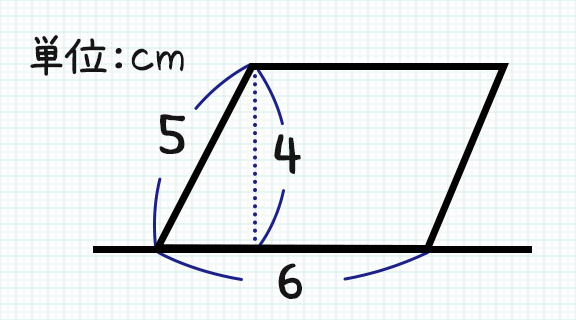



毎日脳トレ この平行四辺形の面積わかる Dアプリ レビュー




簡単公式 ひし形 菱形 の面積を計算できる2つの求め方 Qikeru 学びを楽しくわかりやすく




簡単公式 平行四辺形の角度の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
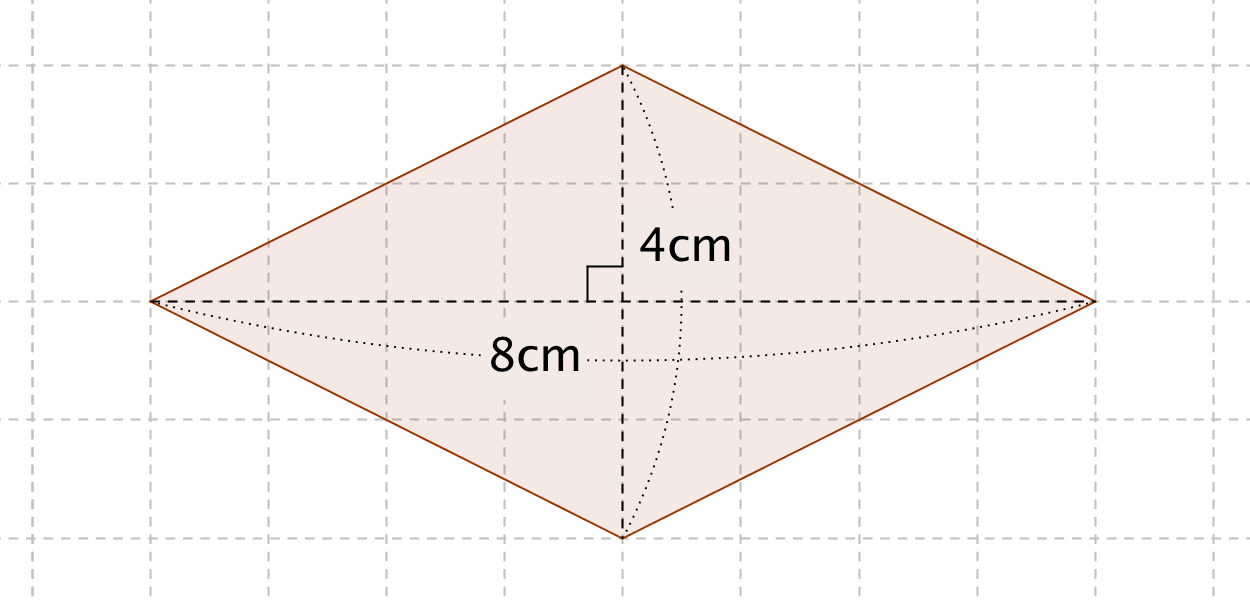



ひし形の面積の公式 算数の公式




高校数学 平行四辺形の面積の求め方 例題編 映像授業のtry It トライイット




平行四辺形のなかの三角形の相似や角度 長さ 等しい面積の求め方 現役塾講師のわかりやすい中学数学の解き方




平行四辺形の面積の求め方 公式と計算例
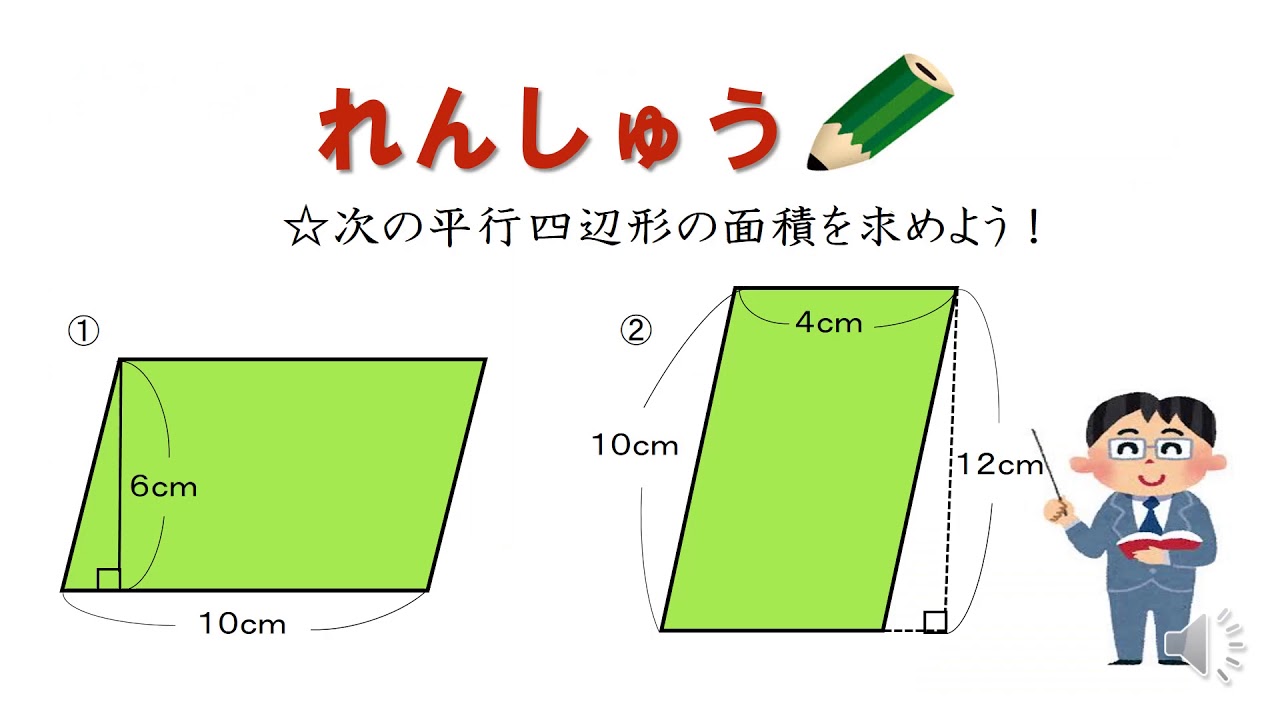



小5 面積の求め方を考えよう 平行四辺形 日本語版 Youtube



1




小5 算数 小5 41 平行四辺形の面積 Youtube
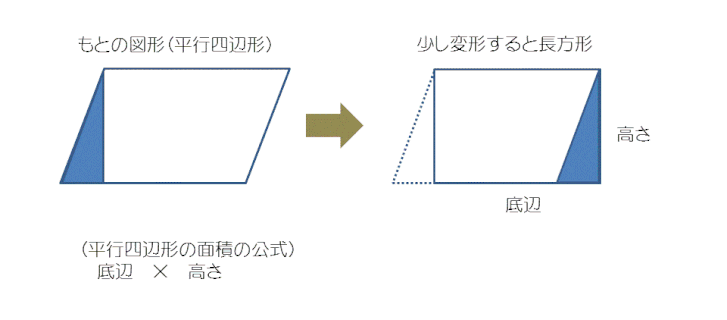



平行四辺形の面積の公式はイメージでとらえること 小学生の子供の成績を上げる方法




平行四辺形の面積を対角線の長さと角度から求める 解説図付き なぜか分かる はかせちゃんの怪しい研究室




ベクトルの外積と平行四辺形の面積 身勝手な主張
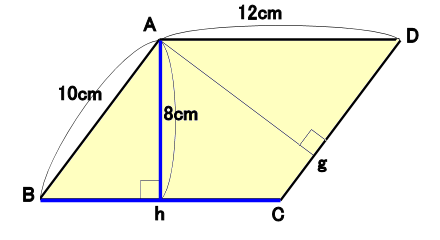



平行四辺形と高さ
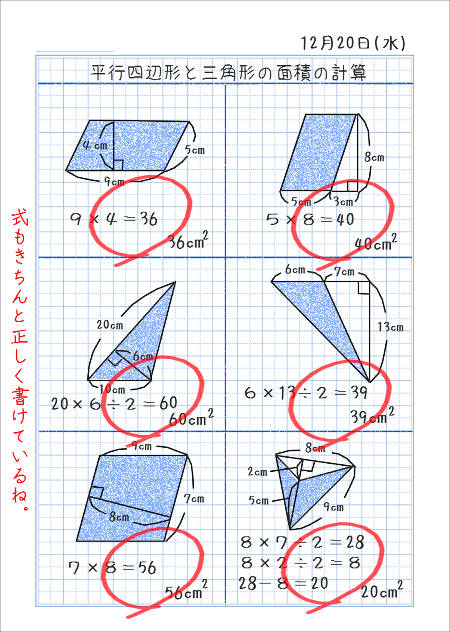



平行四辺形と三角形の面積 家庭学習レシピ
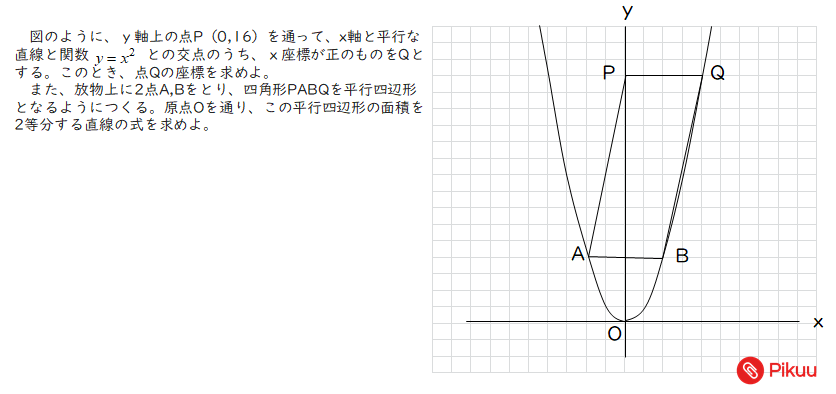



中学数学 平行四辺形の面積を二等分する直線を求める定期テスト予想問題 Pikuu



栃木県総合教育センター 算数 数学 学びの杜 小学校5年生 算数 平行四辺形の面積



平行四辺形の面積計算 ゆるゆるプログラミング




中1数学 比例その8 座標と平行四辺形 明成塾 解説 Youtube
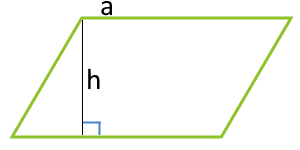



平行四辺形の面積
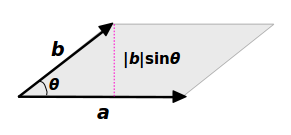



ベクトル積の大きさは平行四辺形の面積 ベクトル解析 基礎からの数学入門
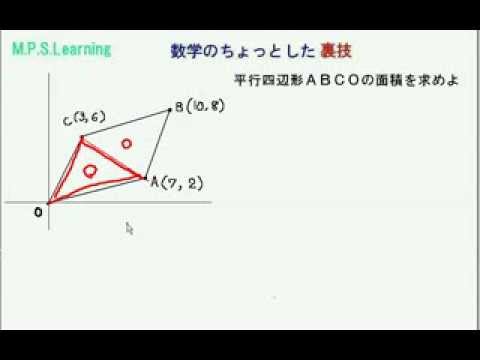



1次関数の応用 平行四辺形の面積 Youtube
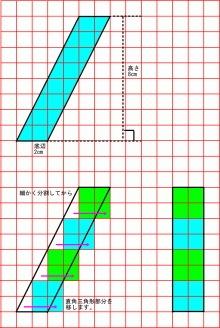



高さが収まらない平行四辺形の面積 15 Do Your Best Haruka Saki
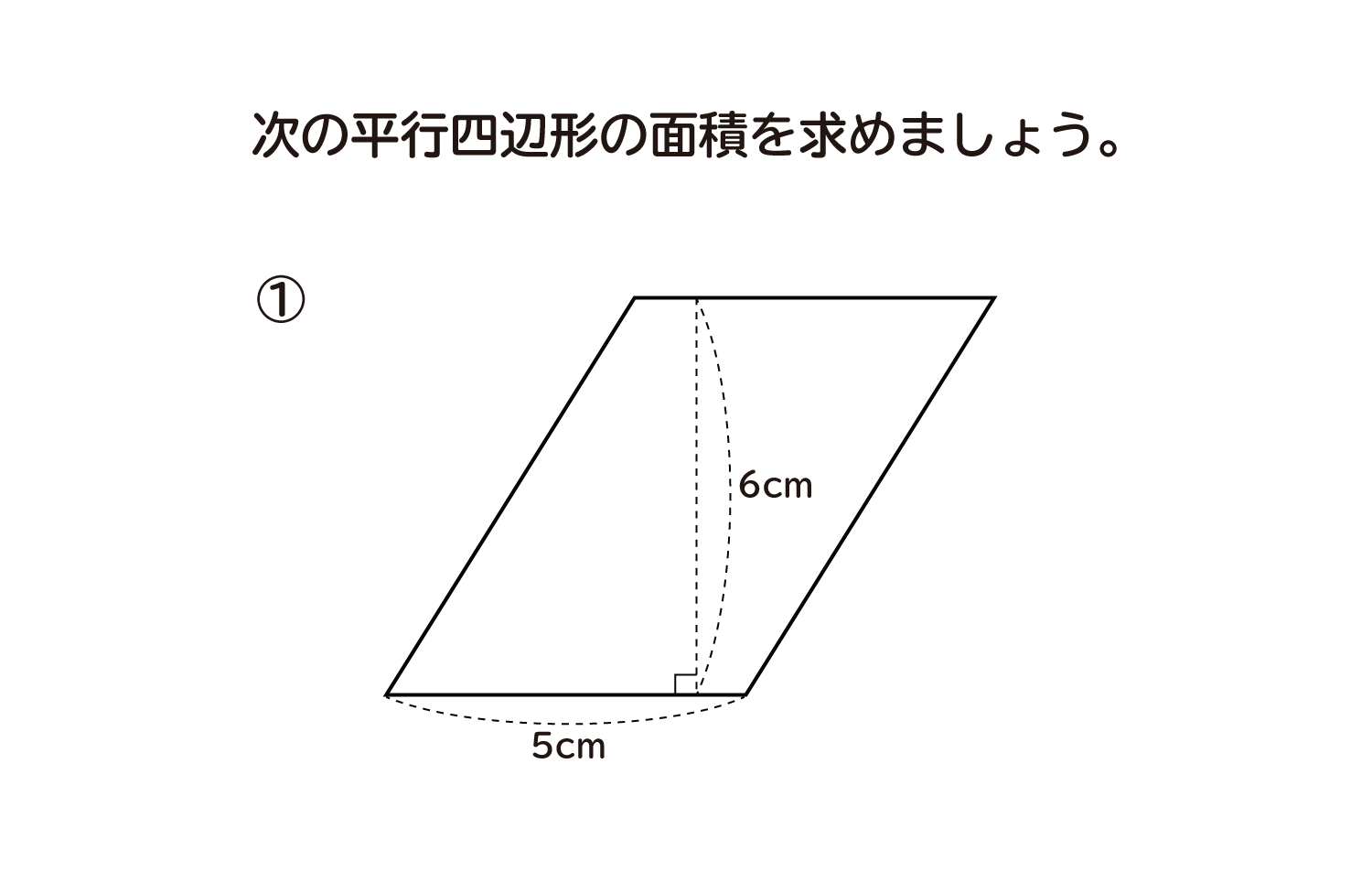



小学5年生 算数 無料問題集 平行四辺形の面積 おかわりドリル




平行四辺形の面積の公式 Note Movies ノートムービーズ
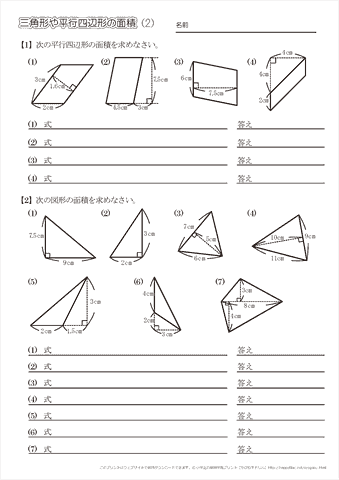



小学5年生の算数 三角形や平行四辺形の面積 問題プリント ちびむすドリル 小学生




平行四辺形の面積の求め方 公式と計算例




平行四辺形の面積の求め方 公式と計算例
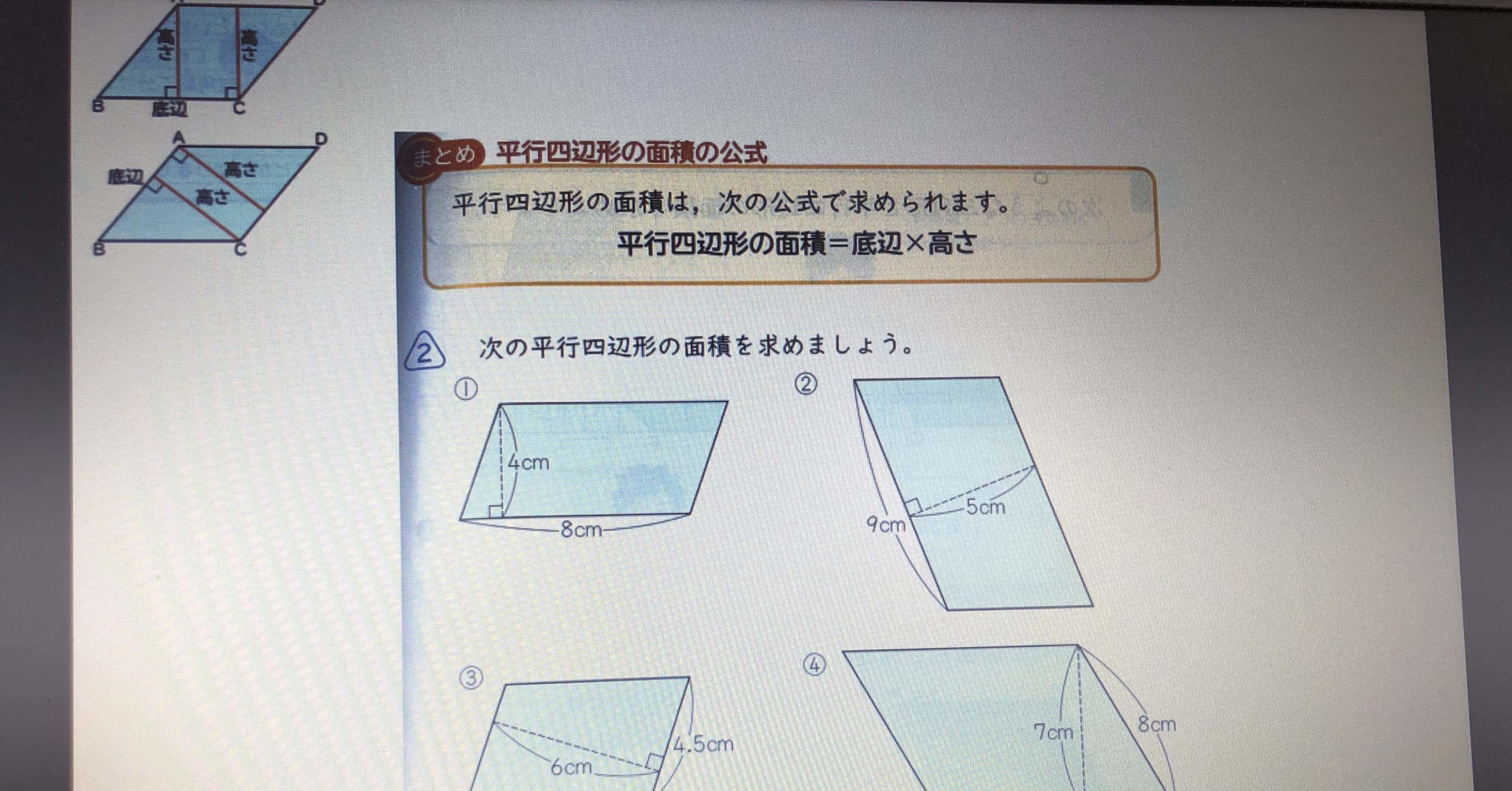



三角形を基に考えるのか 長方形を基に考えるのか 平行四辺形の面積を求める公式 Happy Days From Hakuba Valley Note




平行四辺形の面積の求め方 公式と計算例




ベクトルを用いた三角形 平行四辺形の面積の公式と求め方 高校生向け受験応援メディア 受験のミカタ




ひし形の面積の公式 小学生に教えるための分かりやすい解説 数学fun




平行四辺形の面積の公式 なぜ 底辺 高さ で求められるのか 数学fun



平行四辺形の対角線の折曲げは ねこの耳 から考えよう 算数数学が苦手な子専門のプロ家庭教師みかん先生
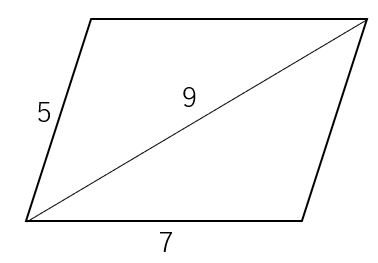



面積 平行四辺形の面積の変わった求め方の問題 数学の要点まとめ 練習問題一覧




平行四辺形の面積公式は覚えない 自分で導き出せるようになろう パパが教える算数教室




関数 グラフ上の平行四辺形の座標 面積 二等分線などの問題を解説 数スタ
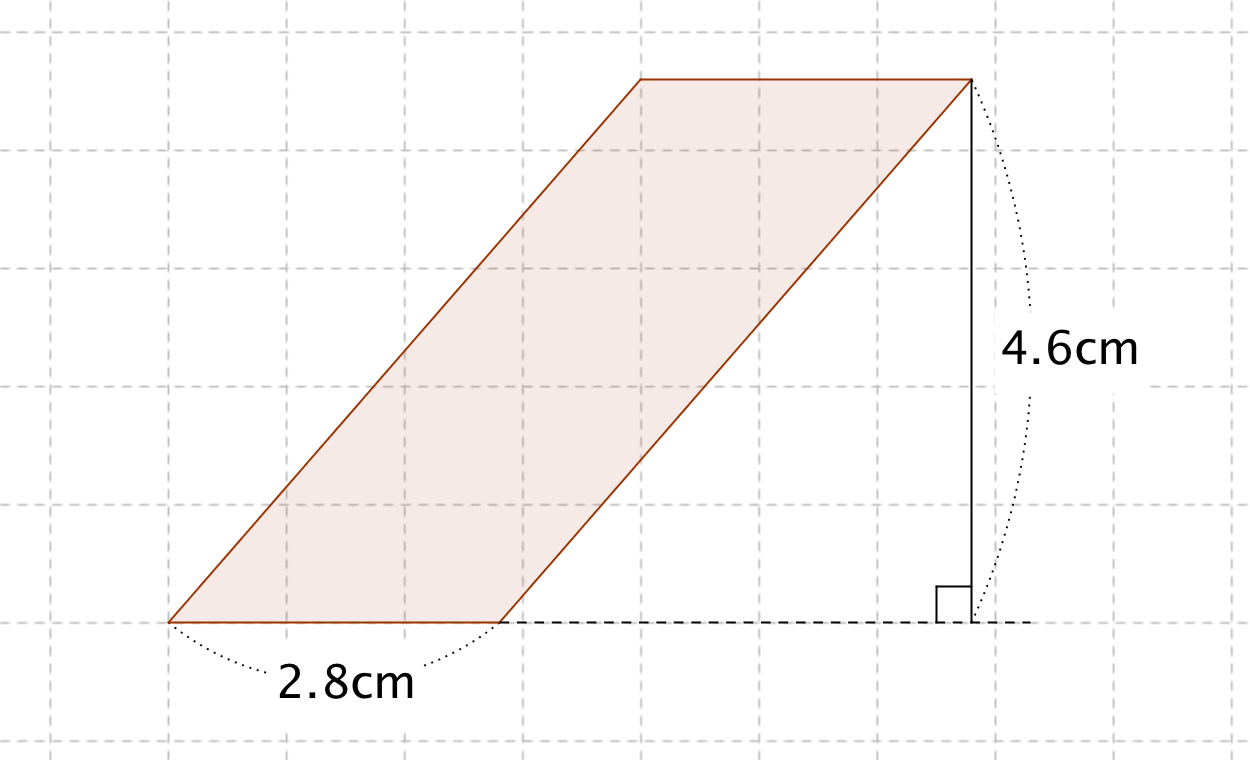



平行四辺形の面積の公式 算数の公式




相似 平行四辺形と面積比の問題を徹底解説 数スタ
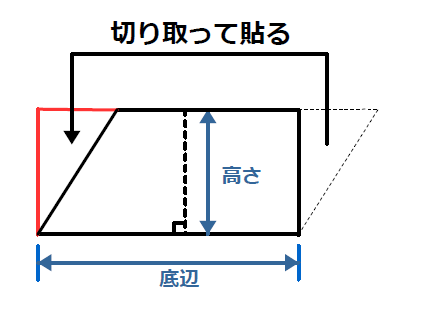



平行四辺形の面積計算 ゆるゆるプログラミング




平行四辺形の面積 算数の公式覚えてますか 算数 面積 気



台形の公式は必要か




四角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ
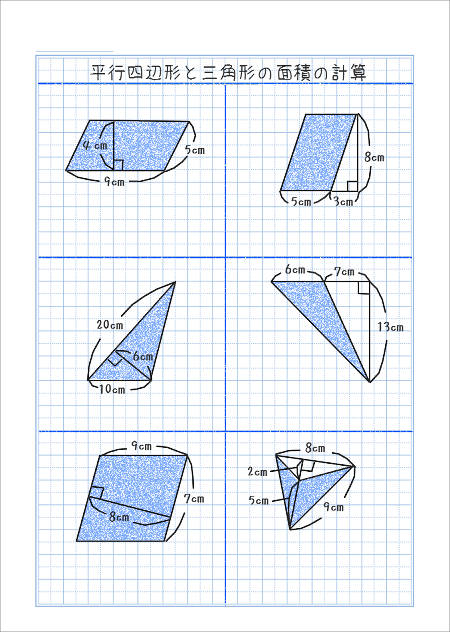



平行四辺形と三角形の面積 家庭学習レシピ




File 平行四辺形の面積2 Png Wikimedia Commons




ボード 勉強 のピン



算数道場 4 面積と体積 1 面積の意味と単位 その7 平行四辺形の面積



1




平行四辺形の面積を求める公式 あまり知られていないかも 中学や高校の数学の計算問題
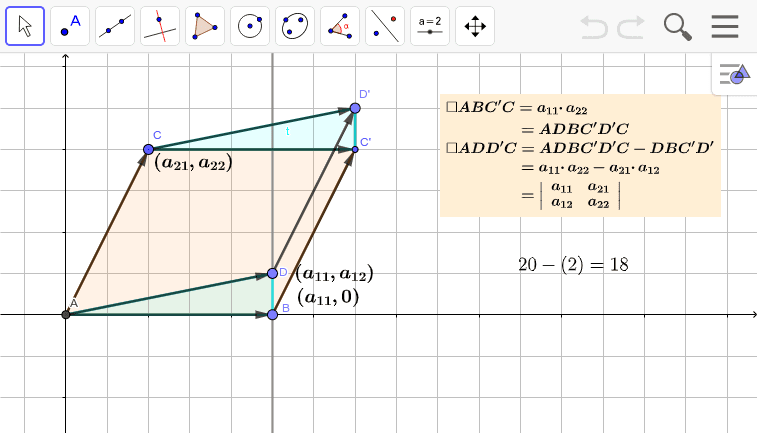



平行四辺形の面積と行列式 Geogebra




平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ



1




簡単公式 平行四辺形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




Descubre Como Resolverlo En Qanda
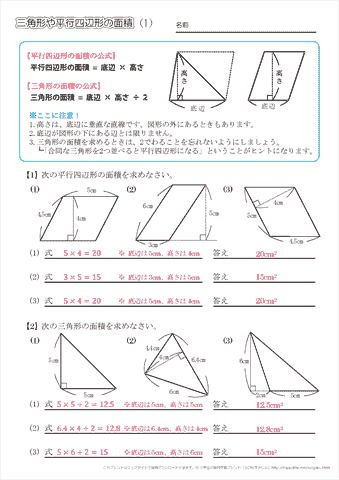



小学5年生の算数 三角形や平行四辺形の面積 問題プリント ちびむすドリル 小学生



お知らせ 中丹教育局
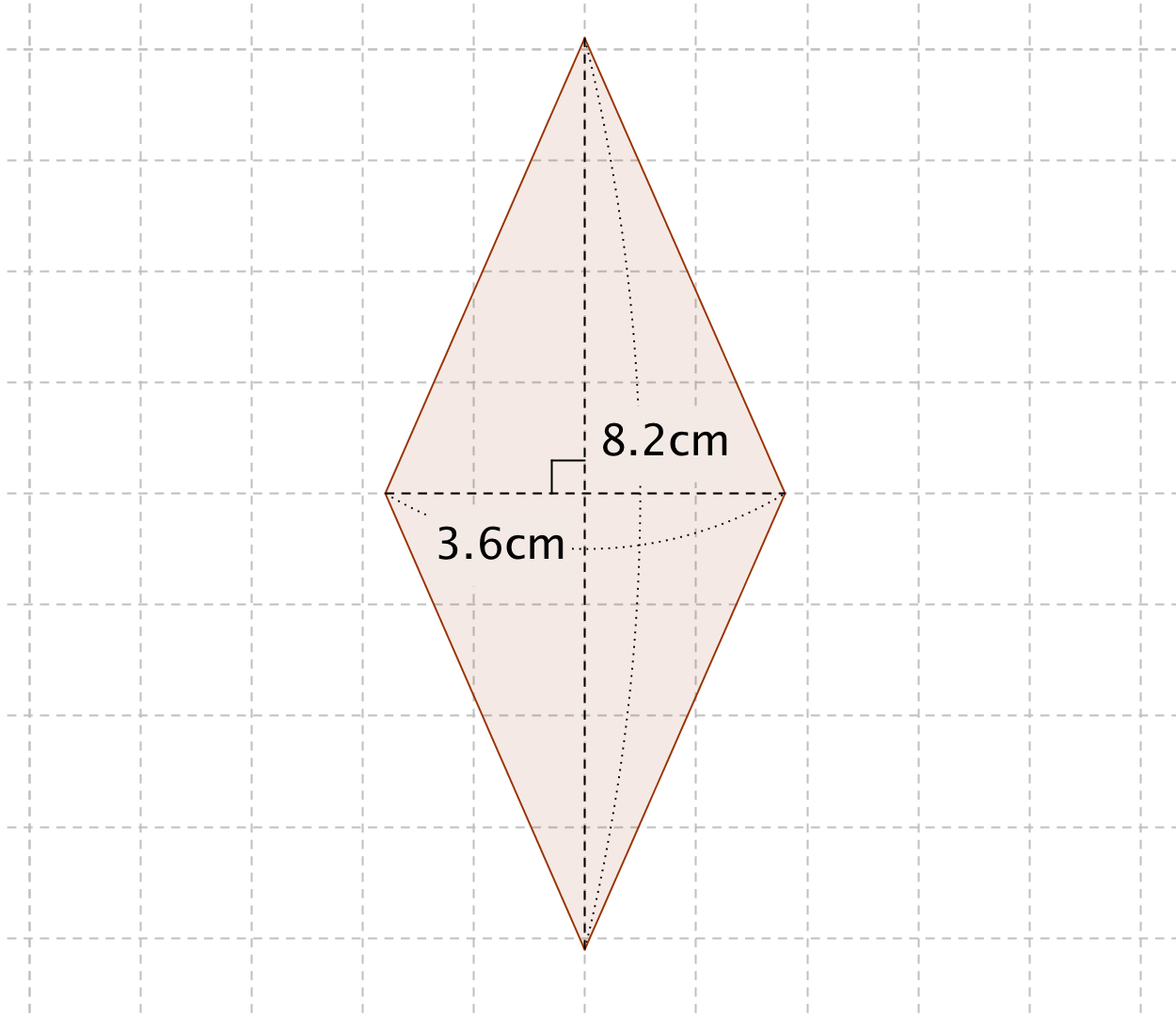



ひし形の面積の公式 算数の公式




四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ
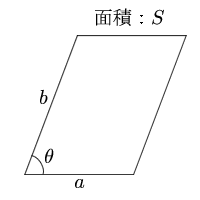



平行四辺形 2辺と間の角度 面積の計算 計算サイト
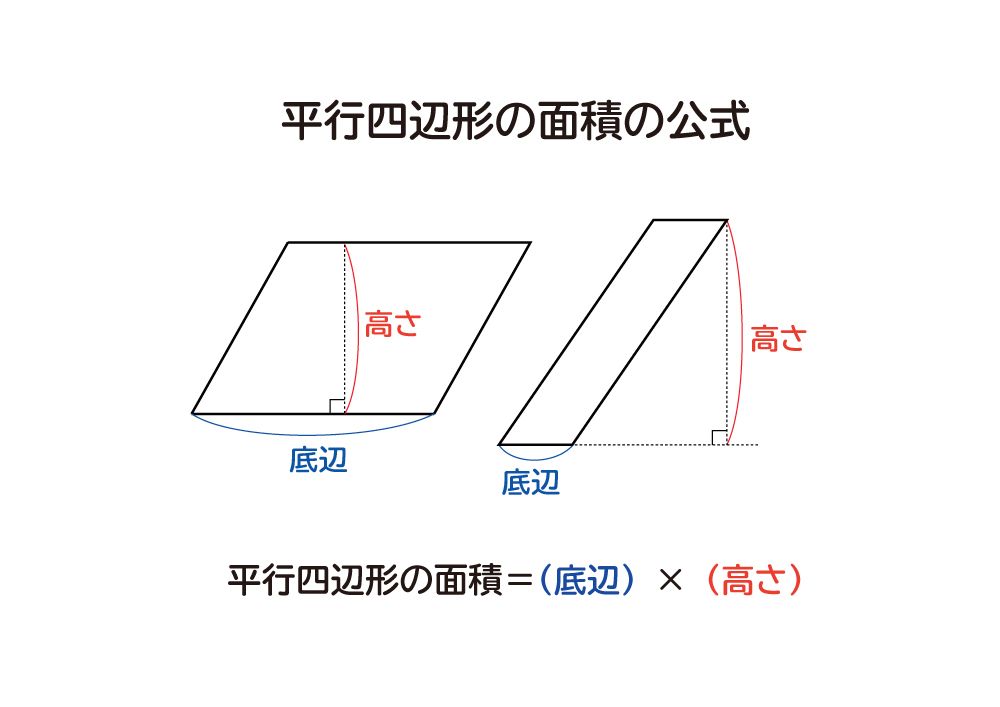



なぜ 平行四辺形の面積は 底辺 高さ なのか を説明します おかわりドリル




動画で学習 1 平行四辺形の面積の求め方 算数




平行四辺形の面積 練習 Youtube




Cm M 1dfrac24 An Descubre Como Resolverlo En Qanda




平方四辺形の面積 小5の問題です 斜線部の面積を求めます 答えは14 小学校 教えて Goo
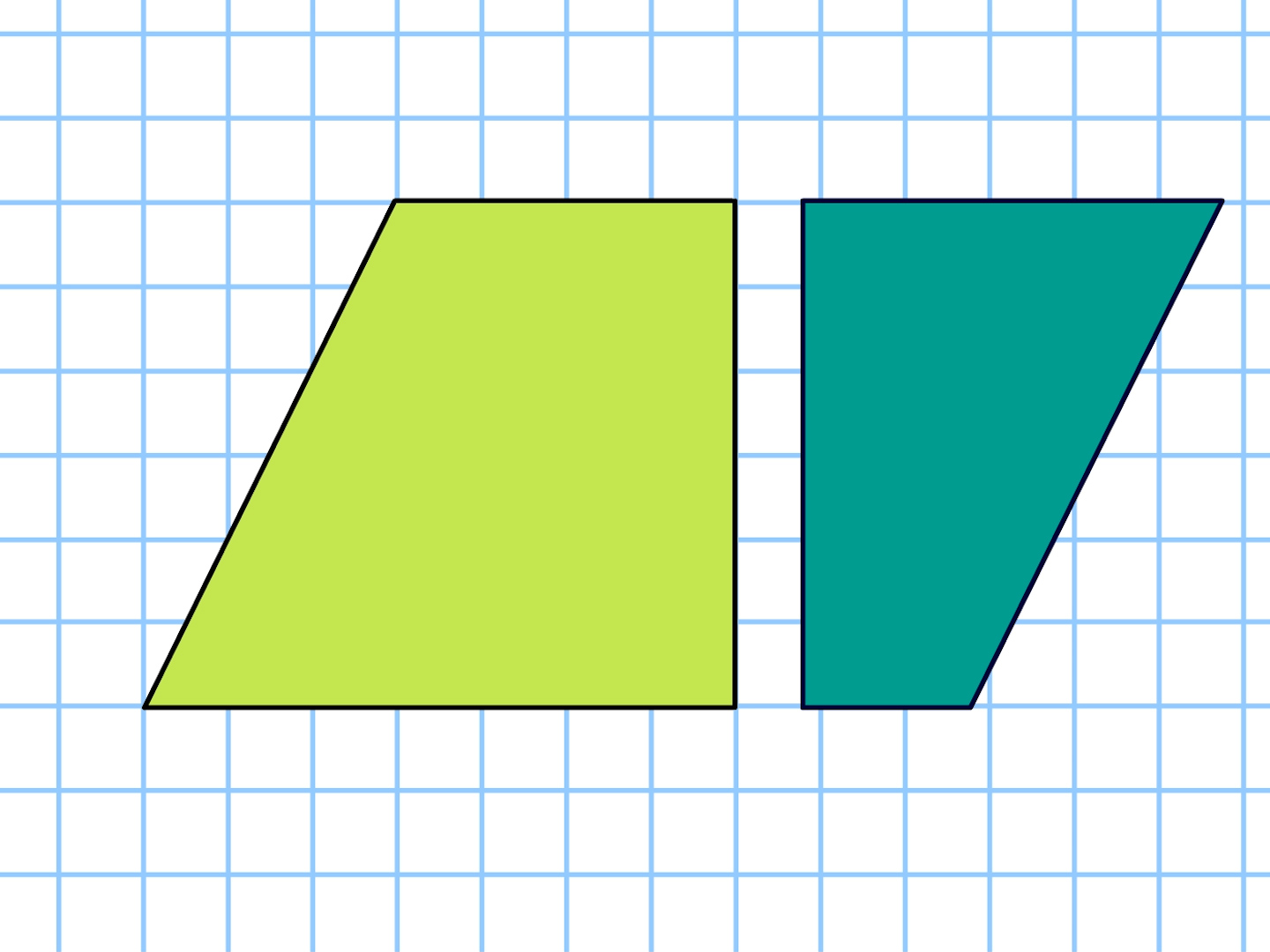



5年 平行四辺形の面積 算数イメージ動画集 大日本図書




ベクトルを用いた三角形 平行四辺形の面積の公式と求め方 高校生向け受験応援メディア 受験のミカタ
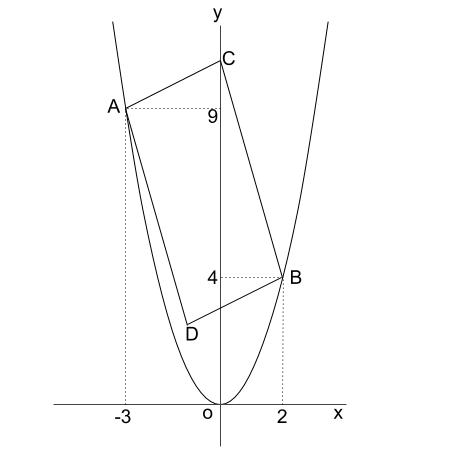



2乗に比例 平行四辺形の面積 中学数学の無料オンライン学習サイトchu Su



0 件のコメント:
コメントを投稿