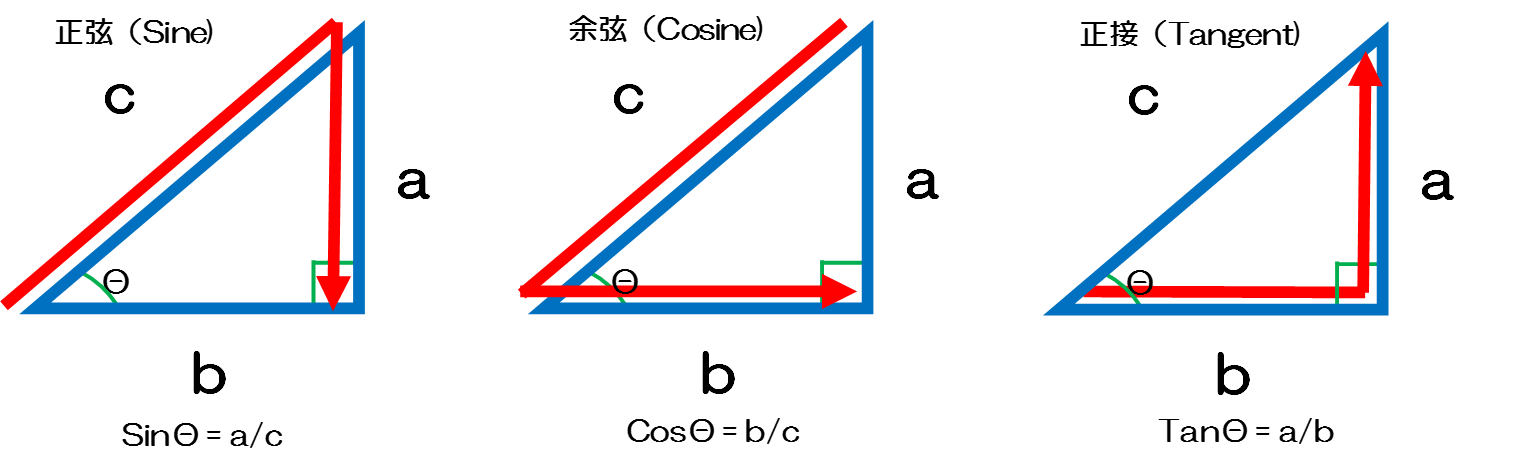
直角三角形の角度の求め方は基本的にcos、sin、tanを用いて求めます。 どれぐらいの知識を有しているのか分からないので2通りのやり方を書きます。 (1)のほうが計算量が少ないかな? (2)のほうが理解しやすいかな?エクセルで tan の値が 173 になる θ を ラジアン解 サイン (sin)、コサイン (cos)、タンジェント (tan)の計算をする前に、三角関数の基本をおさらいしておきましょう。 直角三角形の3辺 a、b、c は、以下のような関係にあります。 例えば、辺cの長さが5で、角度θが30°だった場合、辺aの長さは以下のようになります。 例三角関数(グラフ) sin、cos、tanの関数表を計算し、sinとcosのグラフを表示します。 逆三角関数(度) アークサイン、アークコサイン、アークタンジェントなどの逆三角関数を度単位で計算します。 角度と底辺から斜辺と高さを計算 直角三角形の底辺と傾斜角から斜辺と高さを計算します。 角度と高さから底辺と斜辺を計算 直角三角形の傾斜角と高さから底辺
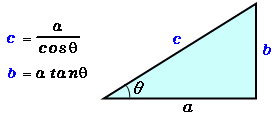
角度と底辺から斜辺と高さを計算 高精度計算サイト
三角形 角度 求め方 tan
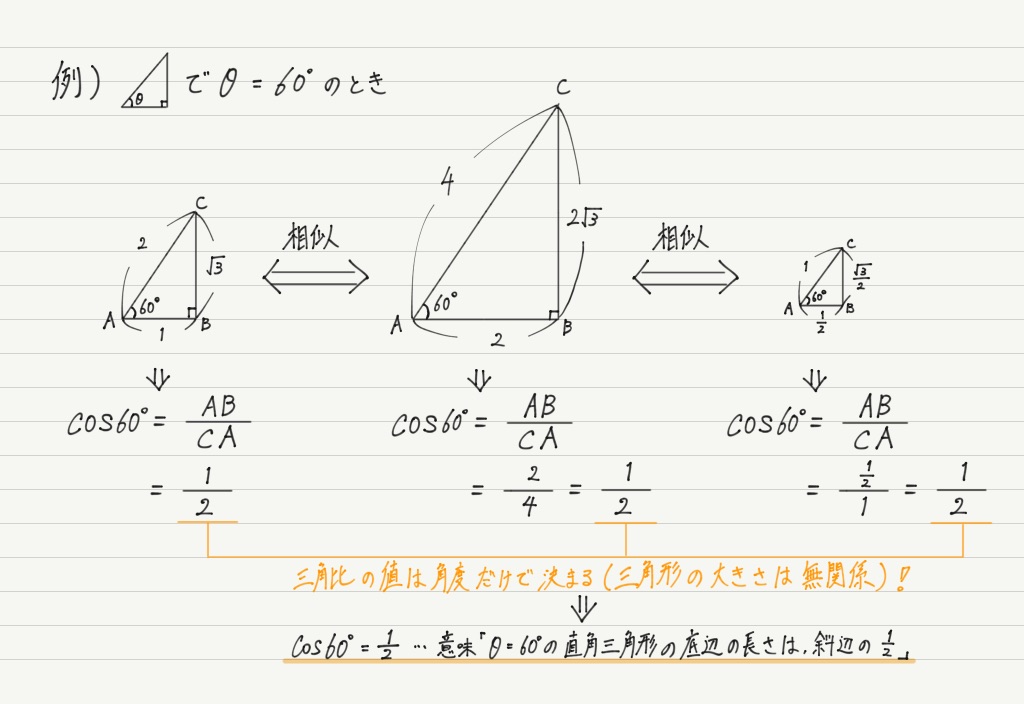
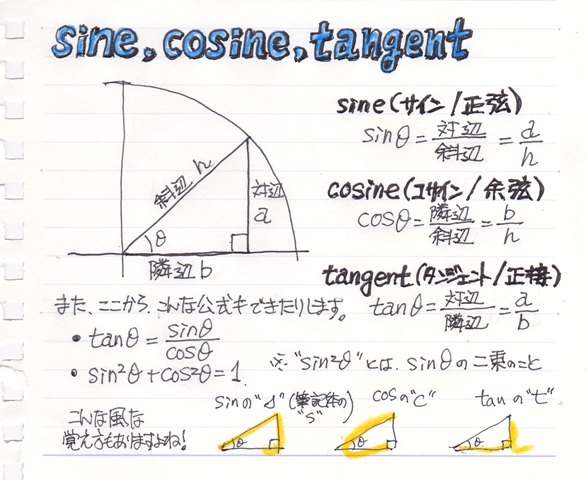
三角形 角度 求め方 tan-2.sin, cos, tanを使ってみよう それでは、下の図形の角度が30度の時の直角三角形の比をsin、cos、tanを使って表してみましょう。 sin何度, cos何度, tan何度という角度は、左端の角度を基準とします。 また、sin、cos、tanを求める時は、三角形の比を使います。 直角三角形の左端の角度が30度の時のそれぞれの辺の長さの比を覚えていますか? 三角形の比についてよくタンジェントとは、直角三角形の1つの鋭角に対する、底辺と対辺の比のことです。 と、言われてもなかなかイメージできないと思うので、下の図を見てみましょう。 直角三角形 ABC(∠A に注目! ) tanA = BC AC tan A = B C A C 上の三角形は、角 C を直角とする直角三角形です。 このとき、辺の比 BC AC B C A C を角 A のタンジェントといい、 tanA tan
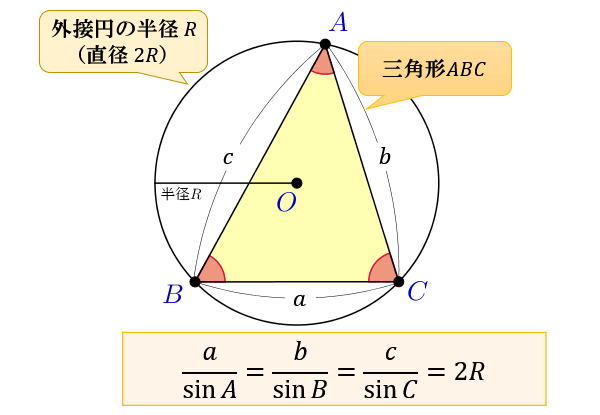



三角比 三角関数の公式一覧 正弦 余弦 加法定理など アタリマエ
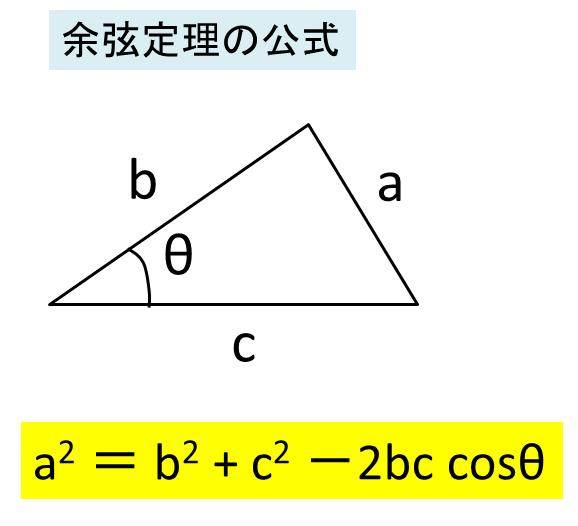
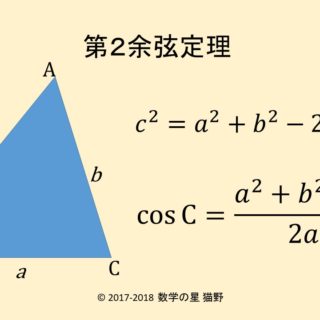
余弦定理を変形すれば、 b , c , a が分かっているときに A を求めるという使い方もできます: a 2 =b 2 c 2 −2bc cos A この式をよく見ると、 「右辺は辺の長さだけ」 でできており、 左辺は角度だけ でできています。 したがって、この式を利用すると 「3辺の 三角比とは? 三角比とは、長さの測量のために生み出された概念で、直角三角形の \(\bf{2}\) 辺の比を角度を使って表したものです。 直角三角形の場合、\(1\) つの鋭角の大きさを決めるとすべての角の大きさが決まり、辺の比も決まります。 三角形の角度を求める時 sin cos tan などを求めて三角比の表を見て角度を求めるといった方法がありますが、その表を使わないで角度を求める方法ってないですか? 三角形の辺すべての長さは分かってい
図1の直角三角形において、角 =30°が先にわかっている場合を考えます。 角 =30°ですから、3つの辺の比は1:2: になり、θ の向かい側の辺が対辺=1、 θに接する辺が底辺= がわかります。 このことを三角関数の tanを使って表すとtan30°= となります。答え 二等辺三角形が2つくっついている問題ですね。 この場合、それぞれの二等辺三角形に注目して角度を1つずつ求めていきます。 赤い二等辺三角形は、頂角が36°なので 底角1つ分の角は となります。 そこから、次は青い二等辺三角形に注目して を直角三角形の角度の求め方 教えて下さい。斜辺以外の2辺の長 直角三角形の角度の求め方は基本的にcos、sin、tanを用いて求めます。 どれぐらいの知識を有しているのか分からないので2通りのやり方を書きます。 二等辺三角形の角度の求め方 厳選6問解説!
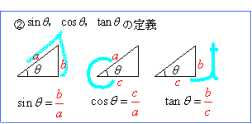
正弦定理から,三角形の辺の長さを求める計算について ABCにおいてa = 3 ,A = 60°,B = 45°のときbを求めよ。 という問題がありますが, これを定理にあてはめていって, b = 3 / sin60°× sin45° まではつくれるんですが,そこから (3 ÷ √3/2 ) × 1/√2= 6/√6=√6 というのになるのが,意味がわかりまSin θ ,cos θ ,tan θ の値は,次の「よく出る2つの三角形」と「sin θ ,cos θ ,tan θ の定義」を覚えていれば導けます。 これらを使った求め方 ① θ の値(角度)を見て,「よく出る2つの三角形」のうち,当てはまる三角形をかき出す。 ②「sinθ,cosθ,tanθの定義」を三角形に当てはめて,辺の比を導く。 ただし,このように導くことがニガテな人は,次の 傾きの求め方は高さを底辺の長さで割れば良い のでしたよね。 三角形OTAにおいては高さは\(sinθ\)、底辺の長さは\(cosθ\)でした。 したがって、\(tanθ=\frac{sinθ}{cosθ}\)と分かります。 また、三角形OT'A'においては高さは\(y\)、底辺の長さは\(x\)でした。



2
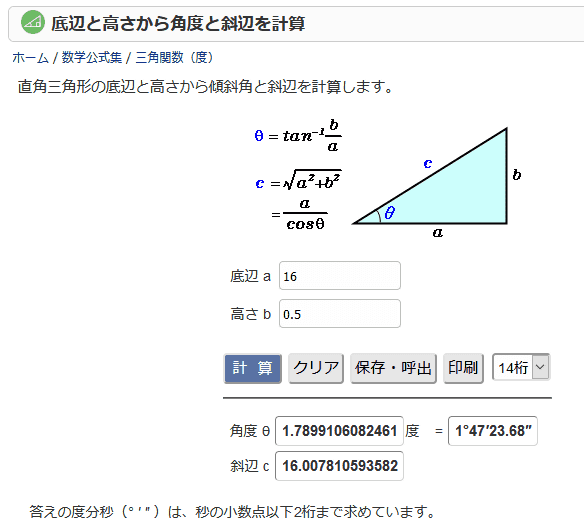



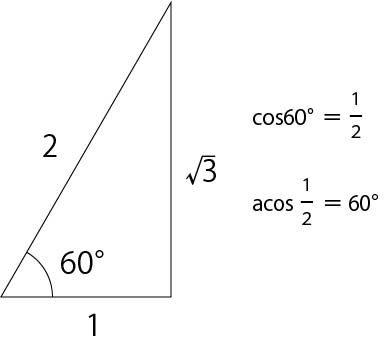
表計算ソフトを使って 底辺 と 高さ から 角度 を求める
T riangle using Heron ′ s formula (1) S =√s(s−a)(s−b)(s−c), s = (abc) 2 (2) if a≥b,c h = 2S a, B=sin−1 h c, C= sin−1 h b if b≥ c,a h = 2S b, C =sin−1 h a, A=sin−1 h c if c≥ a,b h = 2S c, A= sin−1 h b, B=sin−1 h a (3) ABC = 180 T r i a n g l e u s i n g H e r o n ′ s f o r m u l a ( 1) S = s ( s − a) ( s − b) ( s − c), s = ( a b c) 2 ( 2)三角関数から角度 (逆三角関数) タンジェント (正接) tanθから角度 ツイート 三角形の計算 ・ 正三角形 (辺から高さと面積) ・ 正三角形 (高さから辺と面積) ・ 正三角形 (面積から辺と高さ) ・ 直角三角形 (底辺と高さ) ・ 直角三角形 (底辺と斜辺) ・ 直角アークサイン、アークコサイン、アークタンジェントなどの逆三角関数を度単位で計算します。 関数 asin(x) (アークサイン) acos(x) (アークコサイン) atan(x) (アークタンジェント) asin(x) acos(x) atan(x) acsc(x) (アークコセカンド) asec(x) (アークセカンド) acot(x) (アークコタンジェン



1




Excel 三角形の角度を底辺や斜辺 高さから求める方法 直角三角形の角度の計算
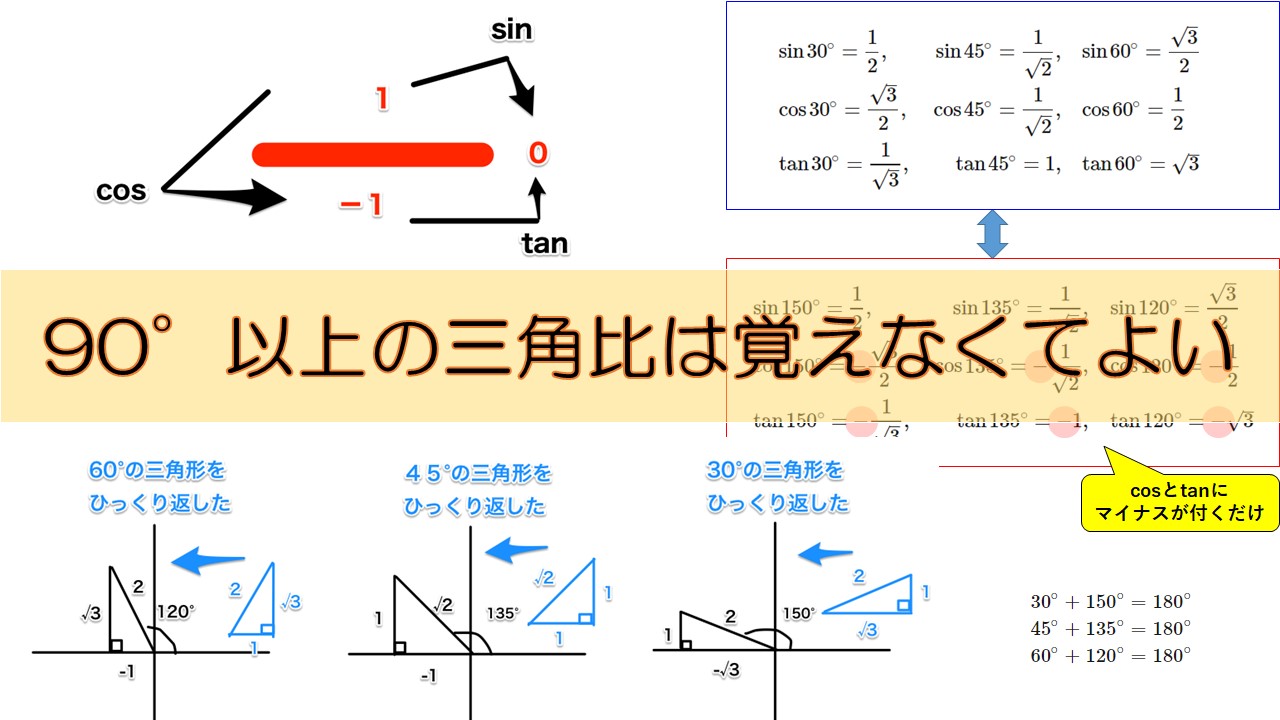
三角形における三角比の値|数学|苦手解決Q&Aのページです。 図形と計量cosの値が負になるときの角度の求め方 図形と計量sinを含む分数の式の計算方法 図形と計量sin,cos,tanの値の覚え方Tanθと直線の傾きは同じ値になることから、θ=45°のとき、直線の傾きは "tan45°=1" (1) θ=60° tanθと直線の傾きは同じ値になることから、θ=60°のとき、直線の傾きは "tan60°=√3" ではもう1問解いてみましょう。 1ページへ戻る 前のページを読む 1/2 最後の公式は少し複雑ですが、頑張って覚えましょう。 1 tan2θ = 1/cos2θ では、おなじみ∠B=30°の直角三角形で考えます。




底辺と高さから角度と斜辺を計算 高精度計算サイト




高校数学 三角比からの角度の求め方3 Tan8 映像授業のtry It トライイット
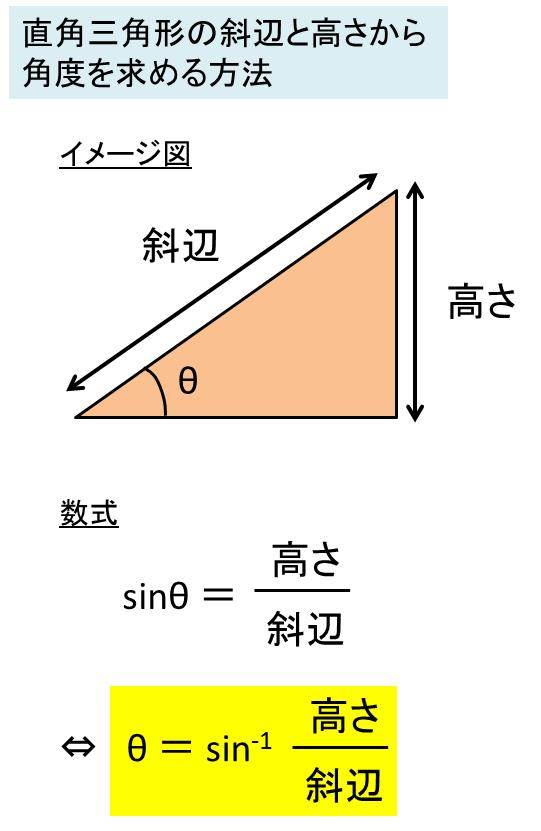
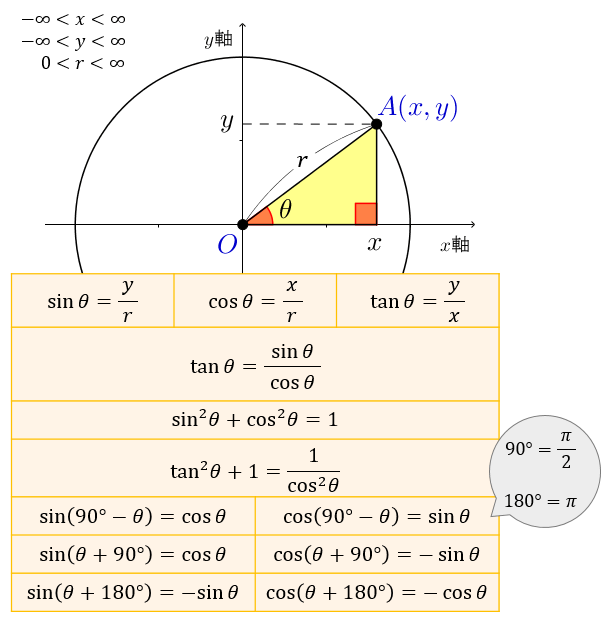
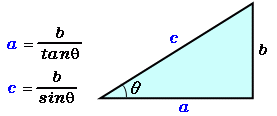
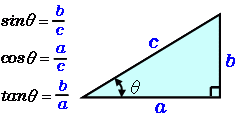
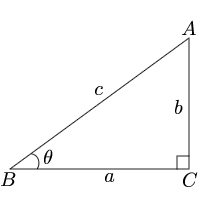
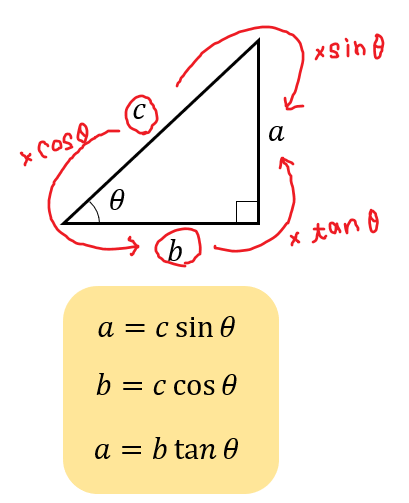
例1直角三角形の高さを求める(sin/radians) 直角三角形の高 直角三角形の高さを求めるための式 さを求めたい 「=11*sin(radians (36))」と入力 三角関数とは逆に「辺の長さから角度を求める」には、逆三角関数を使い ます。答えの度分秒(° ′ ″ )は、秒の小数点以下2桁まで求めています。 Right triangle (1) cosθ = a c , sinθ= b c , tanθ= b a (2) P ythagorean theorem a2b2 =c2 R i g h t t r i a n g l e ( 1) cos θ = a c , sin θ = b c , tan θ = b a ( 2) P y t h a g o r e a n t h e o r e m a 2 b 2 = c 2 <目次> サイン・コサイン・タンジェントの求め方 sin・cos・tanの関係 90 -Aのときのsin・cos・tan 90 +θのときのsin Processingのsin関数とcos関数は、円の半径と角度からサインとコサインの三角比を求めることができる関数となります。




三角関数の知識 やさしい電気回路




高校数学 直角三角形を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 30 45 60 の三角比 受験の月
アドバイス 以上で,tan θ と tan(90°−θ) では,底辺と高さが逆になるのが理解できましたか。 90°−θの三角比を考えるときは,上のような2つの直角三角形をイメージして覚えておきましょう。 それではこれで回答を終わります。これからも,『進研ゼミ高校講座』にしっかりと取り組ん 30°,60°の求め方 正三角形を2つにわけた図形をイメージします。この三角形は30°,60°,90°の三角形で辺の長さの比が12\( \sqrt{3} \)です。これを使って三角比で求めます。 45°の求め方 直角二等辺三角形をイメージします。・直角三角形(高さと角度) 直角三角形の高さと角度から、底辺と斜辺と面積を計算します。 ・直角三角形(斜辺と角度) 直角三角形の斜辺と角度から、底辺と高さと面積を計算します。 三角関数




三角関数は何に使えるのか サイン コサイン タンジェントの活躍 Qiita



三角関数の角度の求め方や変換公式 計算問題も徹底解説 受験辞典
三角形の角度 無料で使える中学学習プリント 三角関数の基礎角度の求め方とは? (sinθ=1/2からθを計算 三角形の面積の求め方まとめ。 タイプ別でわかる公式一覧 三角形の面積は「 \ (底辺×高さ÷2\) 」という公式から求まりますが、この公式以外吹き出し$15^\circ$ の三角比とその周辺 例題でみたように、これらはすべて $15^\circ$ を基準とした \15^\circ,~90^\circ\pm15^\circ,~180^\circ15^\circ\ の三角比なので、$15^\circ$ の三角比から他の角度の三角比は簡単に導ける。・15度や18度などの三角比も計算することができますが、30度や45度よりかなり大変です。 関連:sin15度、cos15度、tan15度の値と求め方 関連:cos72度、sin18度の2通りの求め方 次回は 単位円を使った三角比の定義と有名角の値(0°~180°) を解説します。
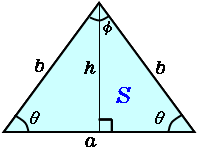



二等辺三角形 高精度計算サイト



Excelで三角関数の計算 Acos関数を使ってみよう パソコンスキルと資格のscワンポイント講座
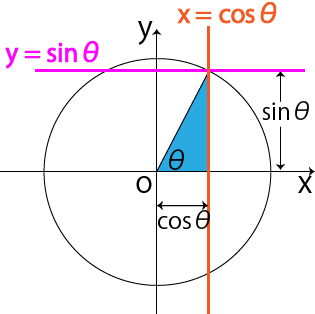
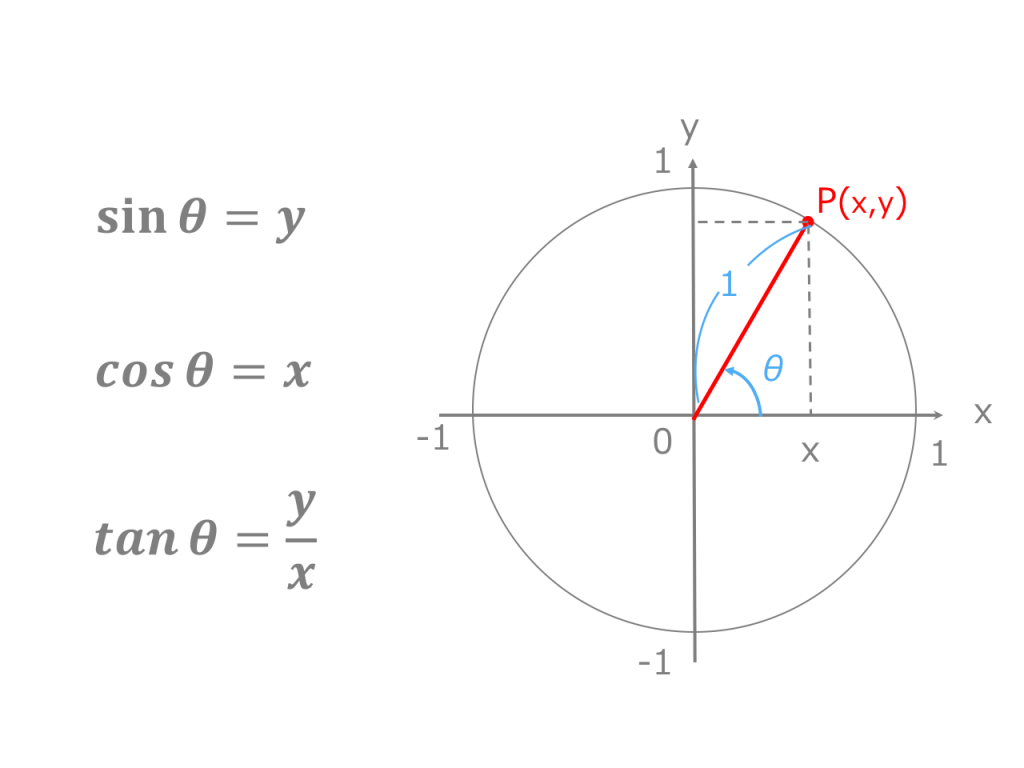
< 鈍角の三角比1 > 角度θが90 以上の場合の三角比を 次で定める。 正の数r に対し,点Q(r,0) を原点 O(0,0) を中心として反時計まわりに角 度θだけ回転した点をP(X,Y) とする。 このとき角度θにおける三角比を sinθ= Y r, cosθ= X r, tanθ= Y X で定める。三角関数の角度は「三角関数の逆関数」を求めることで算定できます。 三角関数y=sinθについて、θ=の形になるような関数を「アークサイン(Arcsin)」といいます。 例えばsin (π/2)=1のとき、逆関数をとるとArcsin (1)=π/2≒157(≒90°)となります。 よって「sinθ=035」のようにθが未知数の場合、アークサインをとることでθを逆算できます。 今回は三角関数の角度の今回はそんな三角関数に関する疑問を解消する角度の求め方の解説です。 スマート ウォッチ 3 メタル バンド 単品 タンジェント(tan)とは、直角三角形の「角」と「辺の比」の関係を表す三角関数の一




三角関数は何に使えるのか サイン コサイン タンジェントの活躍 Qiita




三角関数で角度から座標を導くふたつの式の使い途 Qiita
ちなみに三角比は通常、sin のように、sinやcos、tanに具体的な角度の値を一緒に書く。 (コサイン)の値の求め方 次に、直角三角形においてTanθ=c の求め方 単位円 を用いて θ θ を求める. ただし, θ θ の範囲は π 2 ≦ θ≦ 3π 2 π 2 ≦ θ ≦ 3 π 2 とする. 単位円 を用いた定義では, tanθ = tan θ = y 座標 x 座標 に相当する( ここ を参照). まず,単位円を描き, x =1 x = 1 と x =−1 x = − 1同様にして、特に断り書きがなければ b=AC , c=AB になります。 頂点の名前 A , B , C でその内角∠ A 、∠ B 、∠ C の大きさを表し、単に sin A , sin B , sin C などと書きます。 例 右図において a=BC=8, b=AC=6 , c=AB=7 になります。 (角度が大きいと辺も大きい) 右図のような三角形を描いてみると、3つの角度の中で B が一番大きいとき、その対辺 b は3辺の中で一番大きく



正確な角度の測定 割り付け



タンジェント Tan の求め方を2つ 一歩一歩ぐんぐんブログ
三角関数と逆三角関数の間には、ちょうど反対の関係があります。 sin 30°=05 ←→ Sin105=30° 三角比は、xy平面の力を借りて、基準となる角度が 90° 以上の場合でも考えていくことができる。 三角比では0°から180°の角を、そして「三角関数」では180°より大きい角などに広



Arctan2 アークタンジェント2 ってなんぞ No More Retake



Excel 三角形の角度を底辺や斜辺 高さから求める方法 直角三角形の角度の計算



三角関数の角度の求め方や変換公式 計算問題も徹底解説 受験辞典



三角関数の角度の求め方や変換公式 計算問題も徹底解説 受験辞典




Sin Cos Tan 三角比 三角関数の基礎をスタサプ講師がわかりやすく解説 高校生なう スタディサプリ進路 高校生に関するニュースを配信



三角比と三角関数 高校物理をあきらめる前に 高校物理をあきらめる前に
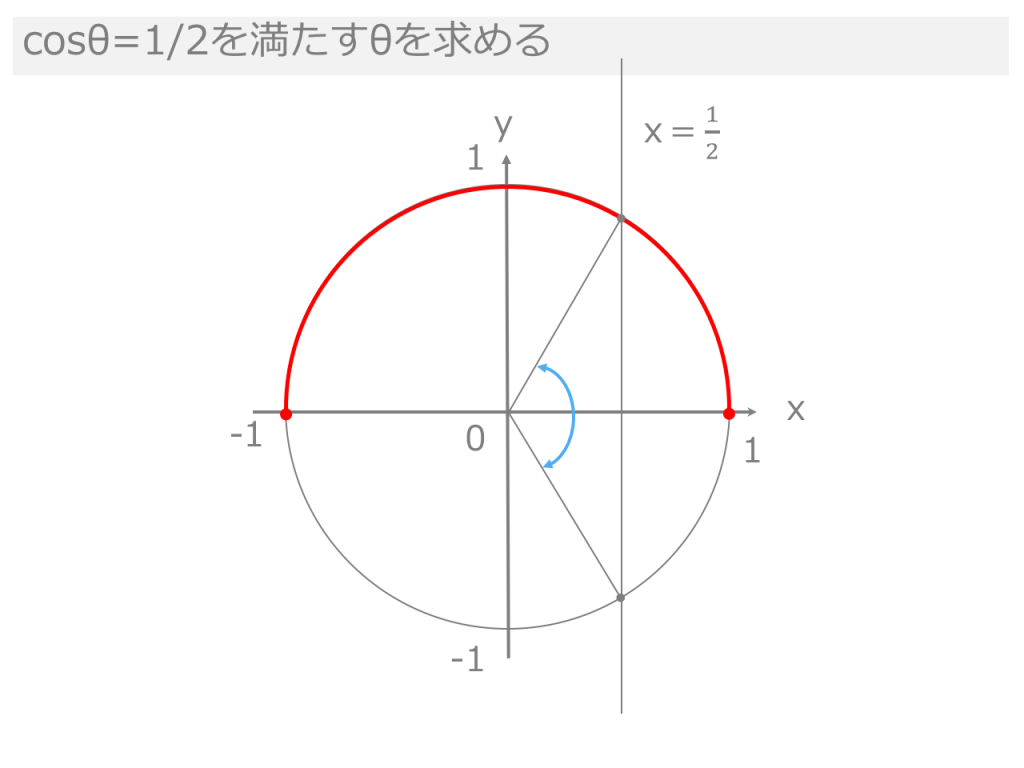



3分でわかる 三角関数の角度の求め方 三角方程式を解く 合格サプリ



3分でわかる 三角関数の角度の求め方 三角方程式を解く 合格サプリ




外接円の半径の求め方がイラストで誰でも即わかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ



サイン コサイン タンジェントの角度の求め方 一歩一歩ぐんぐんブログ



サイン コサイン タンジェントの角度の求め方 一歩一歩ぐんぐんブログ




三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ




高校数学 直角三角形を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 30 45 60 の三角比 受験の月
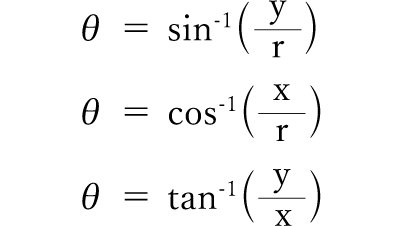



三角関数をマスターしよう その3 金属加工 ものづくり初心者のメモ帳 Mc マシニングセンター Ncプログラムの学習



Sin Cos 1 Cg Mathematics 05yg



高校数学 三角比 三角比の拡張 90 より大きいsin Cos Tanは簡単に求めることができる 数学の面白いこと 役に立つことをまとめたサイト




タンジェントとは何か 中学生でも分かる三角関数の基礎




三角形の辺から角度を計算 製品設計知識



Windows電卓で三角関数を計算する方法 Trismegistuslabo トリメギブログ



三角関数の角度の求め方や変換公式 計算問題も徹底解説 受験辞典




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ



三角関数の角度の求め方や変換公式 計算問題も徹底解説 受験辞典




角度と底辺から斜辺と高さを計算 高精度計算サイト



三角比 三角関数の公式一覧 正弦 余弦 加法定理など アタリマエ




三角関数の基礎 角度の求め方とは Sin8 1 2から8を計算 高校生向け受験応援メディア 受験のミカタ




力の分解 三角比編 高校物理をあきらめる前に 高校物理をあきらめる前に




三角形の辺や角が与えられたとき残りの辺や角を求める方法 数学の偏差値を上げて合格を目指す




高校数学 三角比 三角比を使った三角形の面積の求め方 Sin Cos ヘロンの公式を使った方法 数学の面白いこと 役に立つことをまとめたサイト




三角比 三角関数の公式一覧 正弦 余弦 加法定理など アタリマエ



数学の勉強 三角比



Excel エクセルで余弦定理の計算をする方法 角度や辺の長さを求める



三角関数の角度の求め方や変換公式 計算問題も徹底解説 受験辞典




わかりやすい三角比と基本公式 Irohabook




最高三角形 角度 求め方 中学 最高のぬりえ




三角形のきほんのき 三角関数 中山祐介の土地家屋調査士 測量士補 合格 ブログ




直角三角形の辺を求める Youtube



三角関数で直角三角形の辺の比率を求めてみた サイン コサイン タンジェントとか Excel 三角関数 Haku1569 Excel でらくらく データ分析



角度と高さから底辺と斜辺を計算 高精度計算サイト




高校数学 三角比 三角比を使った三角形の面積の求め方 Sin Cos ヘロンの公式を使った方法 数学の面白いこと 役に立つことをまとめたサイト



三角関数 度 高精度計算サイト



三角関数の基礎 角度の求め方とは Sin8 1 2から8を計算 高校生向け受験応援メディア 受験のミカタ




高校数学 2直線のなす角とtan A B 例題編 映像授業のtry It トライイット



Vba 三角比をもとめる Sin関数 Cos関数 Tan関数 角度をもとめる Atn関数




小5 算数 小5 31 三角形の角 Youtube



Sin Cos Tanの値の覚え方 数学 苦手解決q A 進研ゼミ高校講座



余弦定理で角度を求める方法 数学の星




Sin Cos Tan 三角比 三角関数の基礎をスタサプ講師がわかりやすく解説 高校生なう スタディサプリ進路 高校生に関するニュースを配信



三角関数の角度の求め方や変換公式 計算問題も徹底解説 受験辞典



三角関数の角度の求め方や変換公式 計算問題も徹底解説 受験辞典



三角関数の変換 三角形の計算 計算サイト
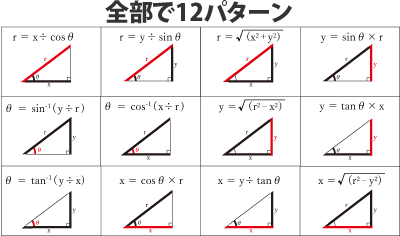



三角関数をマスターしよう その2 金属加工 ものづくり初心者のメモ帳 Mc マシニングセンター Ncプログラムの学習




正弦定理から 三角形の辺の長さを求める計算について 数学 苦手解決q A 進研ゼミ高校講座




余弦定理で角度を求める方法 数学の星




高校数学 三角比 三角比の求め方と覚え方 Sin Cos Tan 数学の面白いこと 役に立つことをまとめたサイト




三角関数の基礎知識



三角関数の角度の求め方や変換公式 計算問題も徹底解説 受験辞典
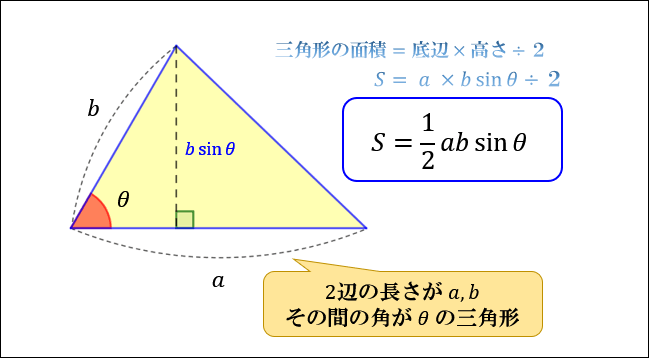



三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ
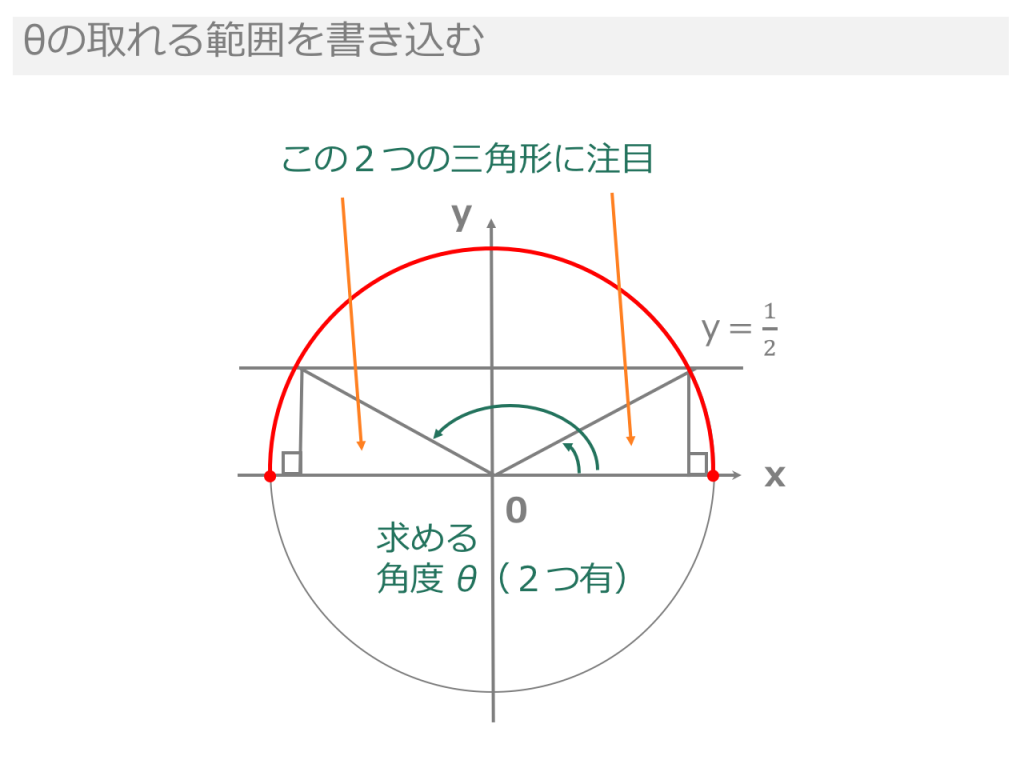



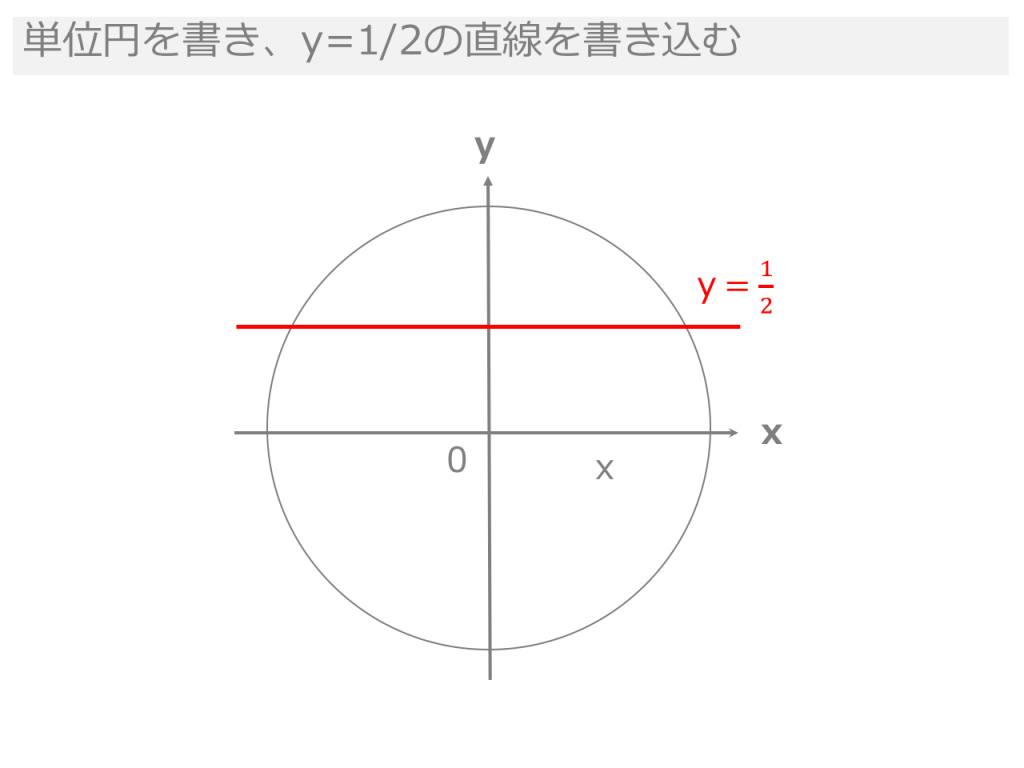
3分でわかる 三角関数の角度の求め方 三角方程式を解く 合格サプリ




わかりやすい三角比と基本公式 Irohabook
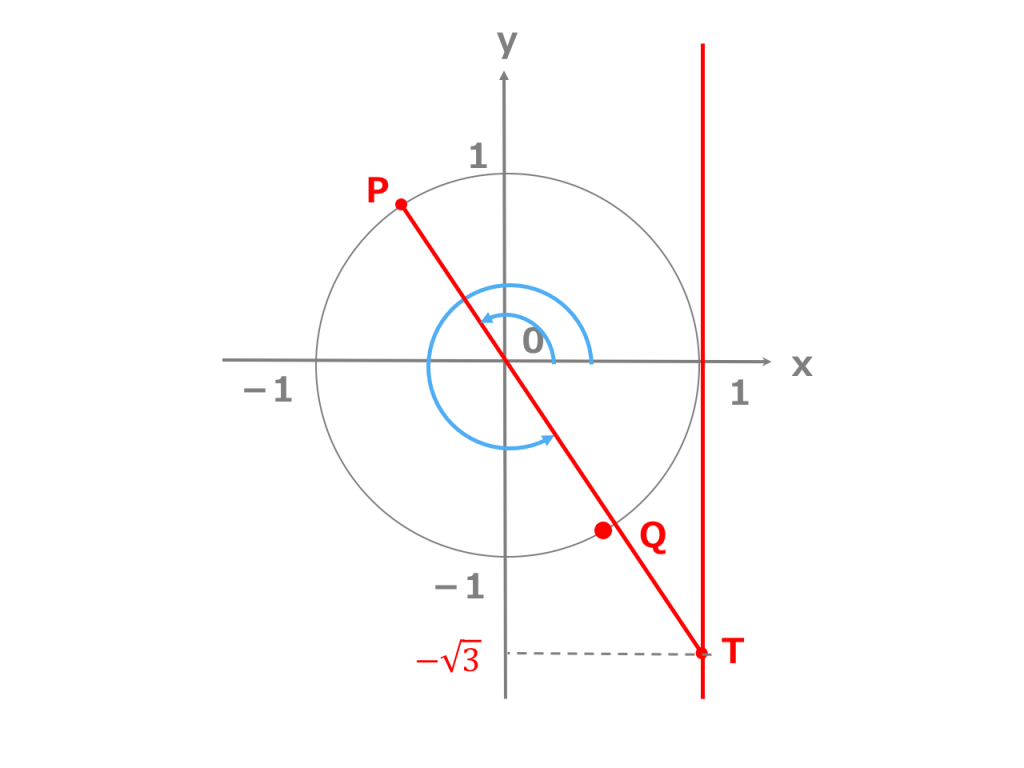



3分でわかる 三角関数の角度の求め方 三角方程式を解く 合格サプリ




高校数学 三角比 三角比を使った三角形の面積の求め方 Sin Cos ヘロンの公式を使った方法 数学の面白いこと 役に立つことをまとめたサイト
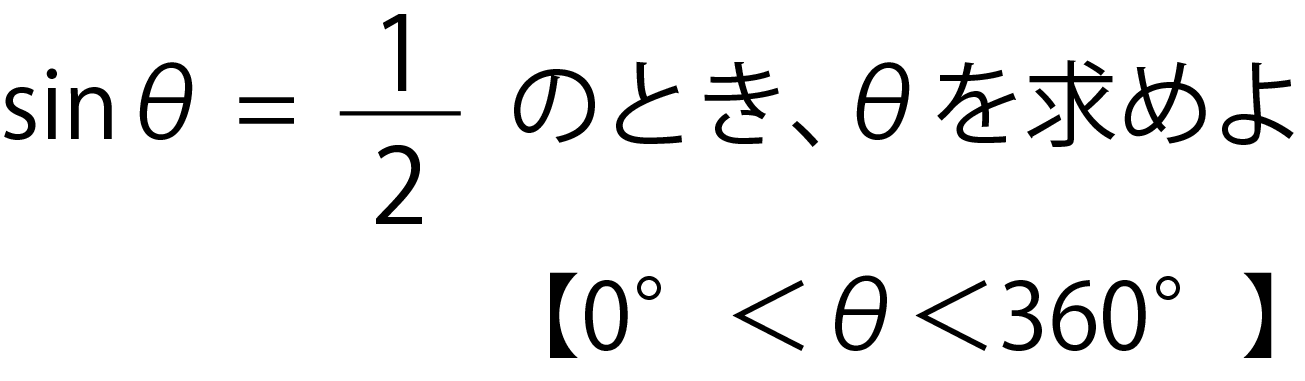



三角関数の基礎 角度の求め方とは Sin8 1 2から8を計算 高校生向け受験応援メディア 受験のミカタ




サインコサインタンジェント Sin Cos Tan とは何を表す 良い覚え方を紹介 遊ぶ数学



高1数学 木の高さを三角比を用いて求める方法を解説 数スタ
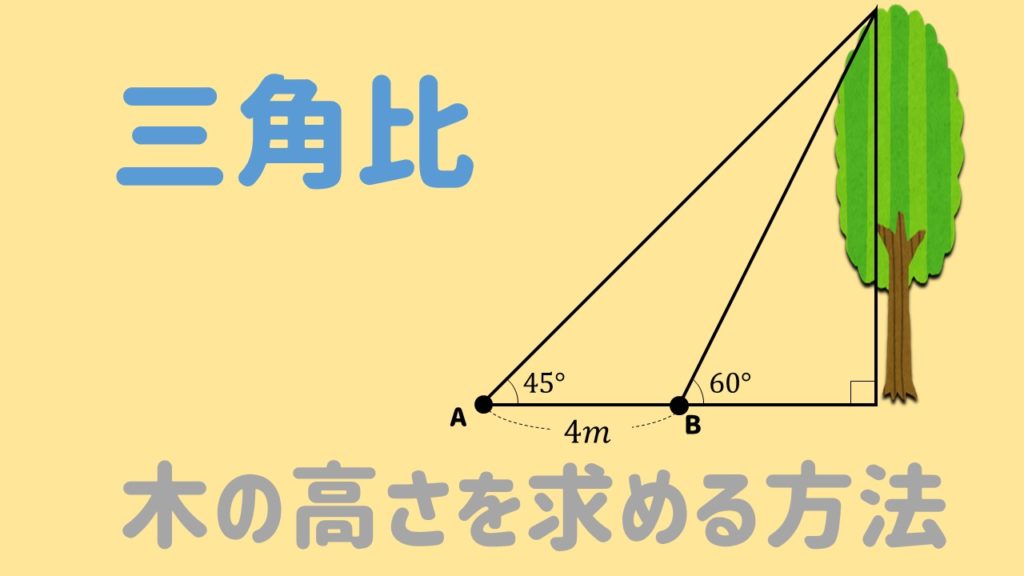



高1数学 木の高さを三角比を用いて求める方法を解説 数スタ



Q Tbn And9gcryolrm Dxfwat4p1nhc1gjbk0qzj6wrbkjapaspbruhs7arqz3 Usqp Cau




三角関数の基礎 角度の求め方とは Sin8 1 2から8を計算 高校生向け受験応援メディア 受験のミカタ
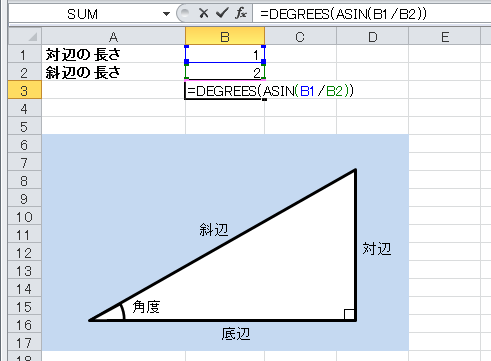



サインから角度を計算するには Asin Degreesの解説 エクセル関数リファレンス
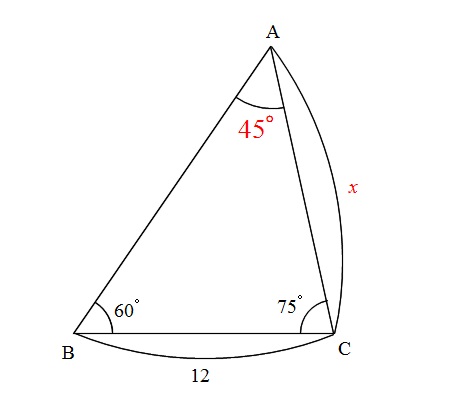



三角形で角度が2つ分かっているのに正弦定理も余弦定理も使えない



1




三角関数 機械加工でよく使う計算方法を説明します セドヤのブログ




3分でわかる 三角関数の角度の求め方 三角方程式を解く 合格サプリ




高校数学 三角比 三角比の求め方と覚え方 Sin Cos Tan 数学の面白いこと 役に立つことをまとめたサイト




底辺と角度から 高さを求める ある高さの木から 10m離れて 木の 数学 教えて Goo
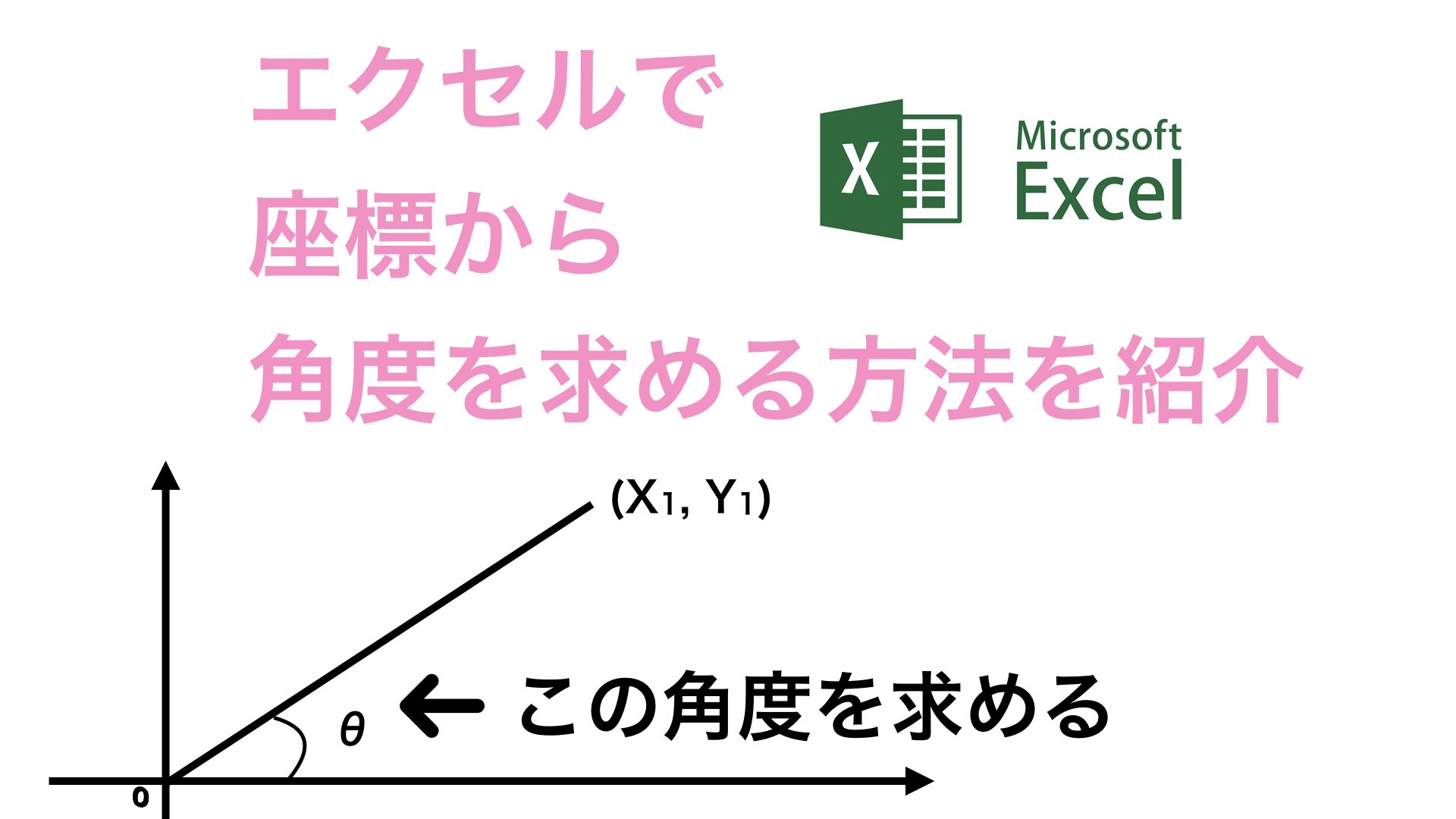



エクセルで座標から角度を求める方法 しおビル
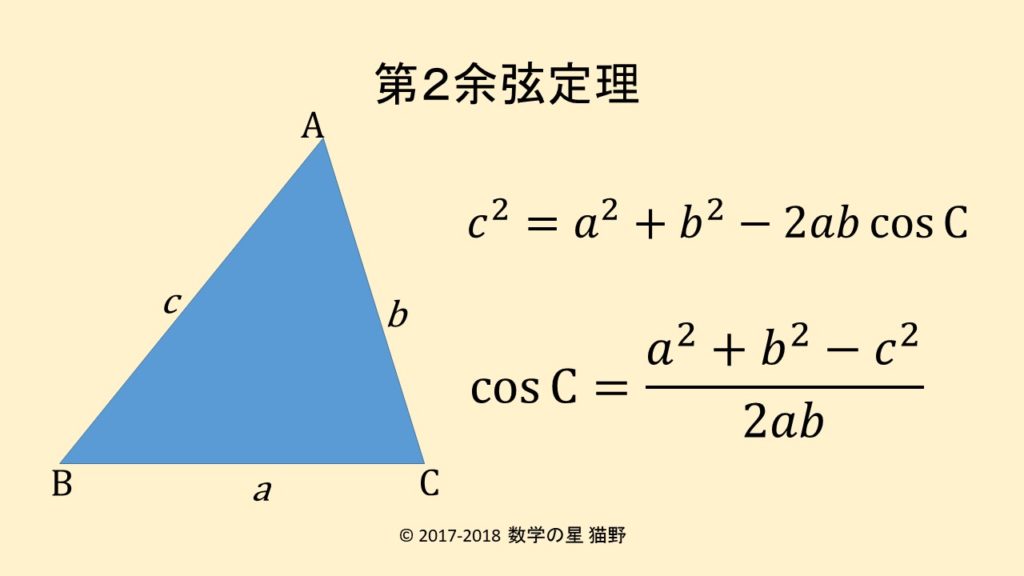



第2余弦定理の公式は辺と角度の関係を簡潔に表す 数学の星



三角関数の角度は 3分でわかる求め方 公式と計算 表との関係




Sin Cos Tan 三角比 三角関数の基礎をスタサプ講師がわかりやすく解説 高校生なう スタディサプリ進路 高校生に関するニュースを配信



1




高校数学 三角比からの角度の求め方1 Sin8 映像授業のtry It トライイット



三角関数の角度の求め方や変換公式 計算問題も徹底解説 受験辞典



直角三角形の角度の求め方 教えて下さい 斜辺以外の2辺の長さが分かっ Yahoo 知恵袋
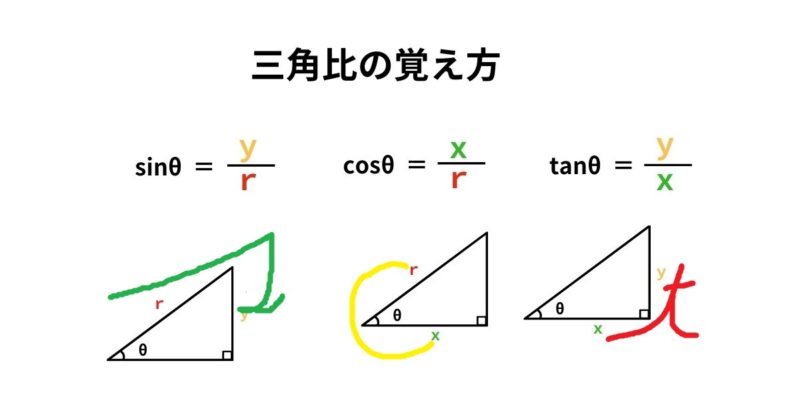



三角関数 機械加工でよく使う計算方法を説明します セドヤのブログ




タンジェントとは何か 中学生でも分かる三角関数の基礎




直角三角形の底辺と高さで角度を求める 電卓で墨だし計算 Teacup ブログ Autopage



サイン コサイン タンジェントの角度の求め方 一歩一歩ぐんぐんブログ




三角関数の基礎知識



3分でわかる 三角関数の角度の求め方 三角方程式を解く 合格サプリ



0 件のコメント:
コメントを投稿