√1000以上 距離 時間 速度 公式 105554-距離 時間 速度 公式

図1 速度による停止距離（1秒の反応時間を含む） 3 辺視」領域からなる。運転者は「周辺視」で路面や景色の「流れ」をとら えて走行状態を確認し、「注視点」で詳細な動きや物体をとらえている」と している。※6 視野に関し、「図2に示されるように、速度が増大すると運転者の視野は 狭くでは実際にこの公式を使ってみましょう。 1．初速度10m/s，加速度50m/s 2 で運動している物体の，時刻70sのときの速度は？ （答） v 0 ＝10， a ＝50， t ＝70 と考えればよいので，これを代入して v ＝10＋50×70＝45 求める速度は 45m/s となります。使用公式從距離和時間計算平均速度 通過距離和時間計算平均速度，以下公式可以為您提供幫助。 1。請輸入以下公式： =a2/(b2*24) 放入要輸出結果的空白單元格，然後將填充手柄向下拖動到要獲取所有結果的單元格，請參見屏幕截圖： 備註：在以上公式中， a2 是距離 b2 是時候了，請根據需要更改

加速度 均速度 减速度和距离已知 如何计算运动时间起点和终点速度为0 中间有加速期 均速期和减速期 距离已知 计算运动时间得用什么公式 谢谢 作业 慧海网

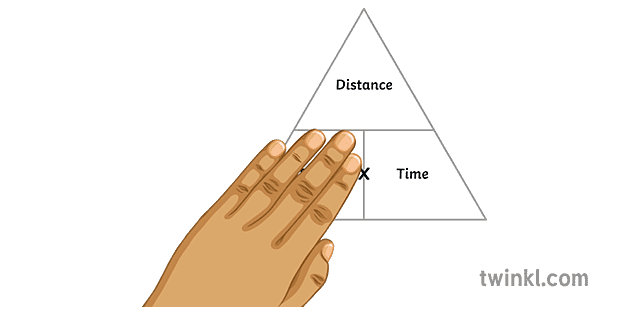
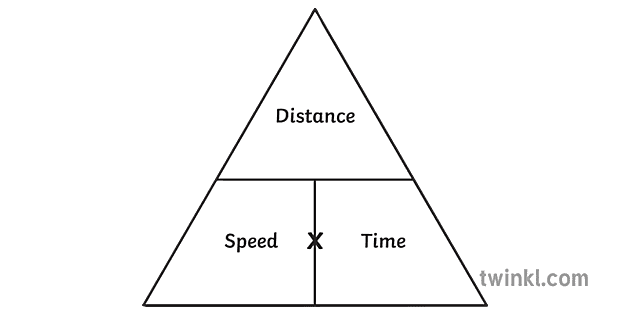
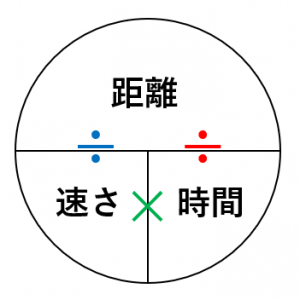
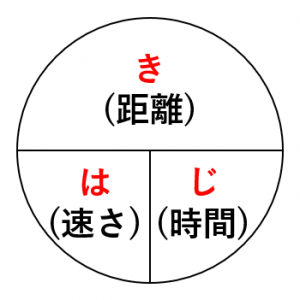
距離 時間 速度 公式

距離 時間 速度 公式- 距離 ＝ 速さ × 時間 速さ ＝ 距離 ÷ 時間 時間 ＝ 距離 ÷ 速さ速度による停止距離 資料6 29 50km/hの場合 30km/hの場合 致死率：約10％ 致死率：80％以上 速度：増大 致死率：上昇 ※Speed management –A road safety manual for decisionmakers and practitioners –より 衝突時の走行速度と歩行者が致命傷となる確率 資料730 運転に必要な情報の90％以上が視覚に依存すると言われ

为什么当速度趋于光速时 无论多远都能瞬间到达 网易订阅

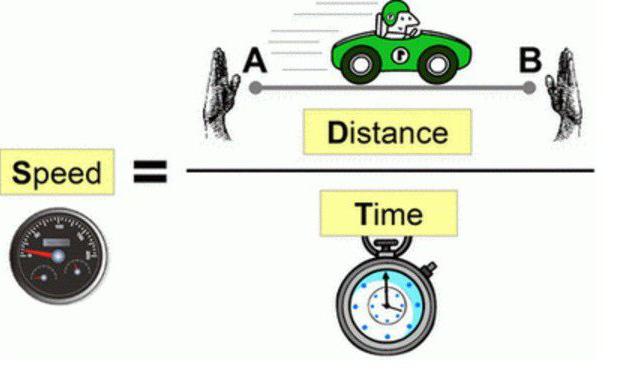
三大公式 初速度 速度 速度 移(長度) 面傾斜角 vo：初速度 v：末速度 g：加速度 S：位移(長 θ：斜面傾 vo：初速度 v：末速度 g：加速度 S：位移(長 θ：斜面傾 a=gsin gsinθ 度a=－g 如何修正 gc V=o0 度) 斜角 gc Vo 度) 斜角 θ sinθ 。 g gsin osθ g gsin osθ 3 θ S θ θ S θ θ S Vo 4 1 時間アメリカテキサス州ヒューストン郊外の住宅地から通勤時間帯の中心部までの平均時速をを求めるため。 距離：286km 時間：25分 平均時速：6864km/h速さ＝距離 ÷ 時間 という公式を使います。 例えば、距離 30 k m の道のりを、 3 時間かけて進んだときの速さは、 距離 ÷ 時間 = 30 ÷ 3 = 10 つまり、 時速 10 k m です。 公式を忘れても、はじきの図で求めたいものを隠すことで、 計算方法 が分かります。 速さを求めたい場合、速さを隠すと、

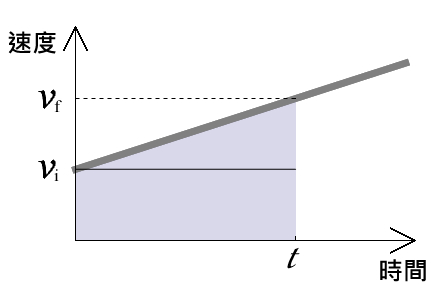
 首先是末速度的公式。 就等速度運動而言，運動的距離等於速度乘以時間，這個想法一點都不困難，但在這裡，我們得用一個「新的眼光」來看待這個想法：函數圖形。如果以速度為縱軸、時間為橫軸的速度－時間關係圖 (vt 圖) 來看，等速度運動的 vt 圖為一條水平的直線，如圖二所示。在這AとBの距離と、AとBの速度を入力し「旅人算を計算」ボタンをクリックすると、出会うまでの時間を求めるための計算方法とAとBが出会うまでの時間が表示されます。 AとBの距離： m Aの速度：分速 m Bの速度：分速 m 360m離れているAとBが向かい合って、Aが分速60m、Bが分速30mで歩きはじめ距離 速さvo、v、加速度a、動いた距離sとの関係式 v 2－v o 2＝2as が導かれた。 Ⅲ ＜速度と加速度＞ dx dv v＝ a＝ dt dt 微分 微分 位置 x 速度 v 加速度 a 積分 積分 運動方程式 ma＝F 微分公式の復習・・次の微分を計算しなさい。ただし、a，b，n、ωは定数

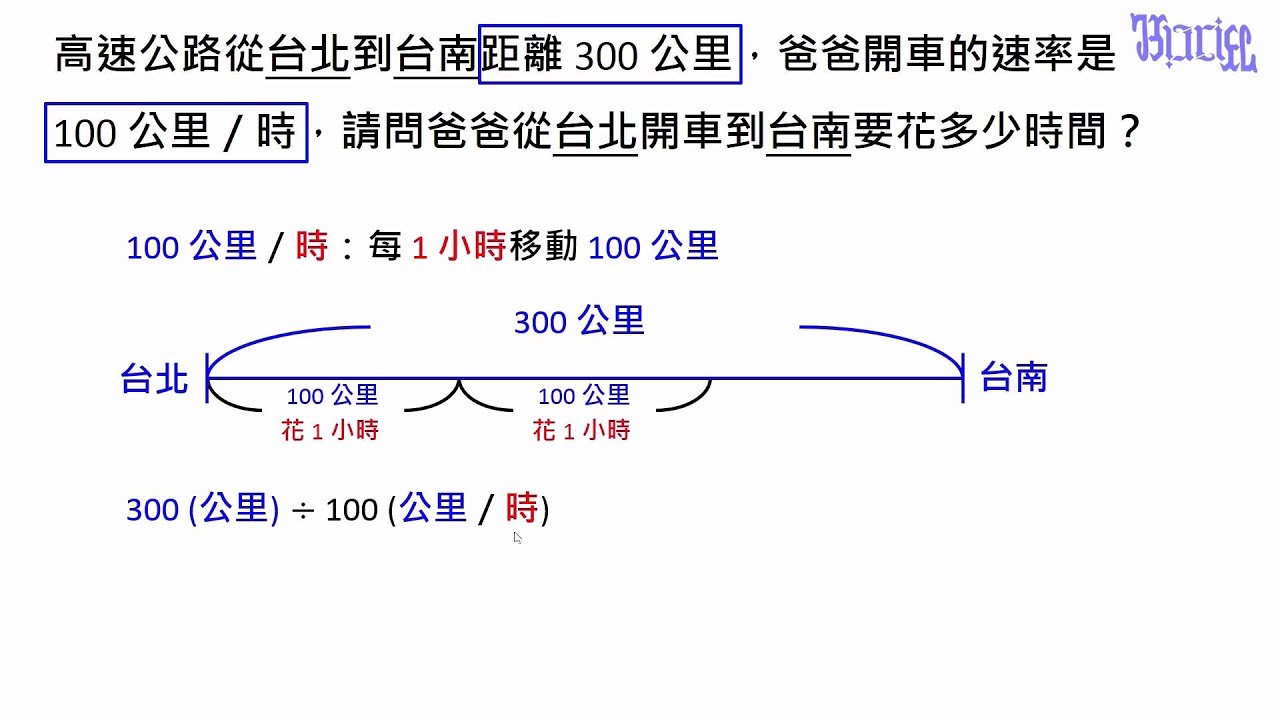
 速さ＝距離÷時間（4＝8÷2） 距離＝速さ×時間（8＝4×2） 時間＝距離÷速さ（2＝8÷4） の3つの公式が成り立っています。 速さ・距離・時間の公式にイメージを持たせる方法時間と速度から距離を求める 時間と速度がわかっていて距離を求めるような場合は、一定期間に進む距離を表した速度にかかった時間を掛けると進んだ距離を求めることができます。式は かかった時間×速度=すすんだ距離 になります。 距離を求める式62 速率、時間及距離的公式 找出 速率 、 時間 及 距離 的 公式有三條： 1距離 ÷ 時間 ＝ 速率 例子1 距離210公里 時間3小時 速率= 210÷3 = 70公里/小時 (70 km/h) 例子2 距離60米

速率教學速率與速度 Pripdw

速度覆蓋的金字塔數學距離時間公式三角形二次 Illustration

停止距離の計算式 ・速度をv0 (m/s)、 摩擦係数をμ、反応時間をta (s) 、重力加速度をg (m/s 2) とします。 ・空走時間 t0 = ta 空走距離 d0 = v0・t0 ・制動時間 t1 = v0/(μg) 制動距離 d1 = v0 2 /(2μg) ・停止時間 t2 = t0 t1 停止距離 d2 = d0 d1 制動時間・制動距離の計算式の誘導 ・車の質量をm（kg）としいういう． 仕事仕事= 力力 ×× 距離距離 ((W=FW = F 摩擦力 初速度v θ mg cosθ s θ mg sinθ μ'mg cosθ h θ mg mg N = mg cosθ 速度v' N 摩擦力初速度 ① 摩擦力 初速度 v mg sinθ μ'mg cosθ h s θ μ θ ② θ mg 速度v' ⎛ ⎞ mvmgh mv'μ'mgcosθs 2 1 2 1 2 ⎟− 2 = ⎠ ⎜ ⎝ ⎝ ⎠ 保存力，非保存力，束縛力 「仕事」と 直線運動の速度と、回転運動の角速度 直線上を物体が移動するときの速度は、単位時間（1秒）あたりどれぐらいの距離 mを進むかで表します。 速度 m/s (メートル毎秒)＝距離 m÷時間 s 図① 上の式より、距離 m＝速度 m/s×時間 s になります

距离公式是多少 科学 21

物理必修1第二章匀变速直线运动的研究1 实验 探究小车速度随时间变化的规律复习练习题 教习网 试卷下载

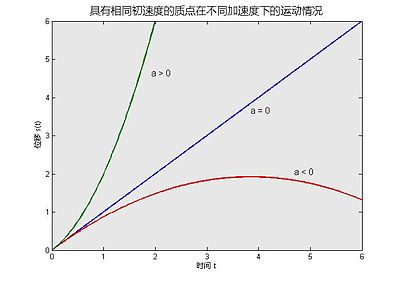
1 移動時間Tを算出するには、目標速度での移動時間と加速時間・減速時間を足すことで求まりますが、まず、「目標速度での移動時間」を求めなければなりません。 2 「目標速度での移動時間」を求めるには、目標速度での移動量を求めます。 それには本單元常用的計算公式整理如表二所示： 3 運動中的物體，其加速度若非定值，則由 Vt 圖形中的曲線可以看出，若 Vt 圖形中速度變化與時間的關係為一傾斜直線，則為「等加度運動」， 反之， 若速度變化與時間的關係為曲線者，則為「非等加度運動」。 4 小学校などで, き・は・じの公式 も習いますが,公式の暗記より,なぜそういう計算をするのか,仕組みを理解することがはるかに重要です さて,60÷15をすると車の速さは, 40km/h だと分かります ここで,距離と速度と時間の関係を考えてみましょう

3种方法来计算初速度

距離速度時間金字塔數學公式三角形次級黑白rgb Illustration

 今回は，力学の基本になる速度と移動距離のお話． 速度とは？ 日本語で言えば，決まった時間でどれくらい進めるかってこと． この時「方向も考える」のが速度 ．方向の概念なしに数字の大きさだけでいいのは「速さ」． 同じ時間で進める距離が大きいほど，同じ時間で長い距離進める速さ・時間・距離 距離 速さ × 時間 = 距離 速さ 距離 ÷ 時間 つまり、 距離 時間 速さ 距 離 時 間 = 速 さ 時間 距離 ÷ 速さ つまり、 距離 速さ 時間 距 離 速 さ = 時 間 この表のとおりですから、公式を覚えるより簡単ですね。 45 k m の車で 3 時間一定の速度で走り続けたとき、何 k m 先まで進みますか。 表に数字をいれればすぐに式ができますね。 45 × 3Find local businesses, view maps and get driving directions in Google Maps

高等数学 手撕牛顿莱布尼茨公式 Coder梁 博客园

赛马娘 比赛时赛马娘的速度和加速度是如何计算的 你点的属性到底有啥用 哔哩哔哩

ボールの速度は次の公式で求められることになります。 v = gt v 速度 t 時間 距離 上のような速度ー時間グラフでは、面積は距離を表します。 上図のように速度が変わらない場合、距離（ボールが動いた距離）は速度×時間で求められます。これはグラフでいうと面積にあたります。 面積（初速度と停止距離の関係を求める） この加速度は一定ですから、等加速度直線運動の時間を含まない式（v 2 v 0 2 = 2ax）を立てますと、 0 2 v 0 2 = 2aS ⇔ 0 2 v 0 2 = 2μ'gS ∴ v 0 2 = 2μ'gS ∴ v 0 2 = 2μ'gS （この式を読み解きますと） 動摩擦係数 μ' が同じ場合、初速度 v 0 が2倍にな公式：速率*時間=距離 1輸入速率 Km/h 公里/時 m/min 公尺/分 cm/s 公分/秒 2輸入時間 h小時 min分 sec秒 3

速度 速率 6年級數學 Grade 6 Math Velocity Youtube

位移 速度與加速度 维基教科书 自由的教学读本

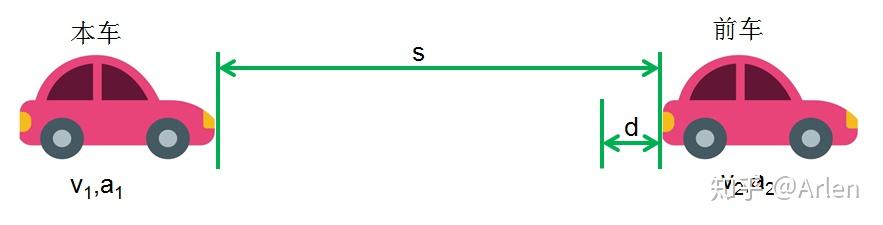
加速度 a 、速さ v求める速度 （時速） 走行距離(m)÷1000÷走行時間(秒)×60×60＝ Km/h （ m/s）走行時間 T＝ 2S / V（Sは走行距離，vは速度） 走行時間(t)＝( 2*距離(m）/ (時速(Km/h)*1000/60/60) 速度から停止距離／スリップ痕から速度を計算する 車両相互の速度，距離関係を計算する 前提となる交通工学基礎知識（解説） 交通事故における車速と停止距離に関する判例集 1108 1308 Ver3

4种方法来求出速度

加速度 均速度 减速度和距离已知 如何计算运动时间起点和终点速度为0 中间有加速期 均速期和减速期 距离已知 计算运动时间得用什么公式 谢谢 作业 慧海网

距離（ x ）を時間（ t ）で微分すると、速さ（ v ）になる 。 \displaystyle 速さ：v = \lim_ {\Delta {t} \to 0} \frac {\Delta {x}} {\Delta {t}} = \frac {dx} {dt} 速さ（ v ）を時間（ t ）で積分すると、距離（ x ）になる 。 \displaystyle 距離（変位）：x = \int v \,dt Point! 『速さ』を初っ端から公式で教えられたのなら それはこの先の不幸の始まりかもしれません。 大事なことは、「距離÷時間」を通して 『どのような意味の値』が求まるのかを 知っていることが大切なのです。 では、割り算なのですから、 「距離÷時間」を計算すると どんな値が導き 等加速度運動の3公式 まず，等加速度運動とは読んで字のごとく各方向で加速度が一定である運動のことです。 速度と加速度，また運動を記述するにあたり必要な時間の導入については こちらのページ を参考にしてください。 教科書にも出てくる重要な

小球沿足够长的斜面向上做匀变速运动 依次经a B C D到达最高点e 已知ab 6 M 1 M 小球从a到c和从c到d所用的时间都是2 S 设小球经 易学啦

计算平均速度 建议 July 21

主軸回転速度350min1 、カッタの外径ø125で切削している、このときの切削速度を求めると、 （答え） 公式にπ=314、DC=125、n=350を代入すると、 vc=(π×DC×n)÷1000=(314×125×350)÷1000 =1374(m/min) これにより、切削速度は、約1374m/min となります。 1刃当たりの送り(fz) vf(mm/min) 1分間当たりのテーブル送り時間 = 速さ です。たとえば、10kmの道を、2時間で移動すれば、速さは5km/hになります。(km/hは、一時間あたりのキロ数=時速を示す) 距離と時間から速さを計算 その運動においては、加速度や動いた距離、速度を求めるための3つの公式が知られています。 初速度v0(m/s),t(s)秒後の速度をv(m/s),加速度をa(m/s² ),t秒間に動いた距離をx(m)とします。 それぞれの公式について意味を説明します。 ①は最も基本となる式です。加速度が一定なので、t秒間で速度はatだけ変化します。

位移 速度與加速度 维基教科书 自由的教学读本

速率 11 速率的三大計算公式 Youtube

 初期微動継続時間は震源からの距離に比例する って言えるね。 初期微動時間が長いほど震源からの距離も大きくなるってことだ。 初期微動継続時間・震源までの距離・地震発生時刻の公式をまとめておこう 以上が自身の地震の計算問題の解き方だよ。

Aeb安全模型 一 基于碰撞时间的安全模型 知乎

如何找到速度公式 自然科学21

速率 08 速率 時間 距離 Youtube

时间距离算速度公式 百度知道

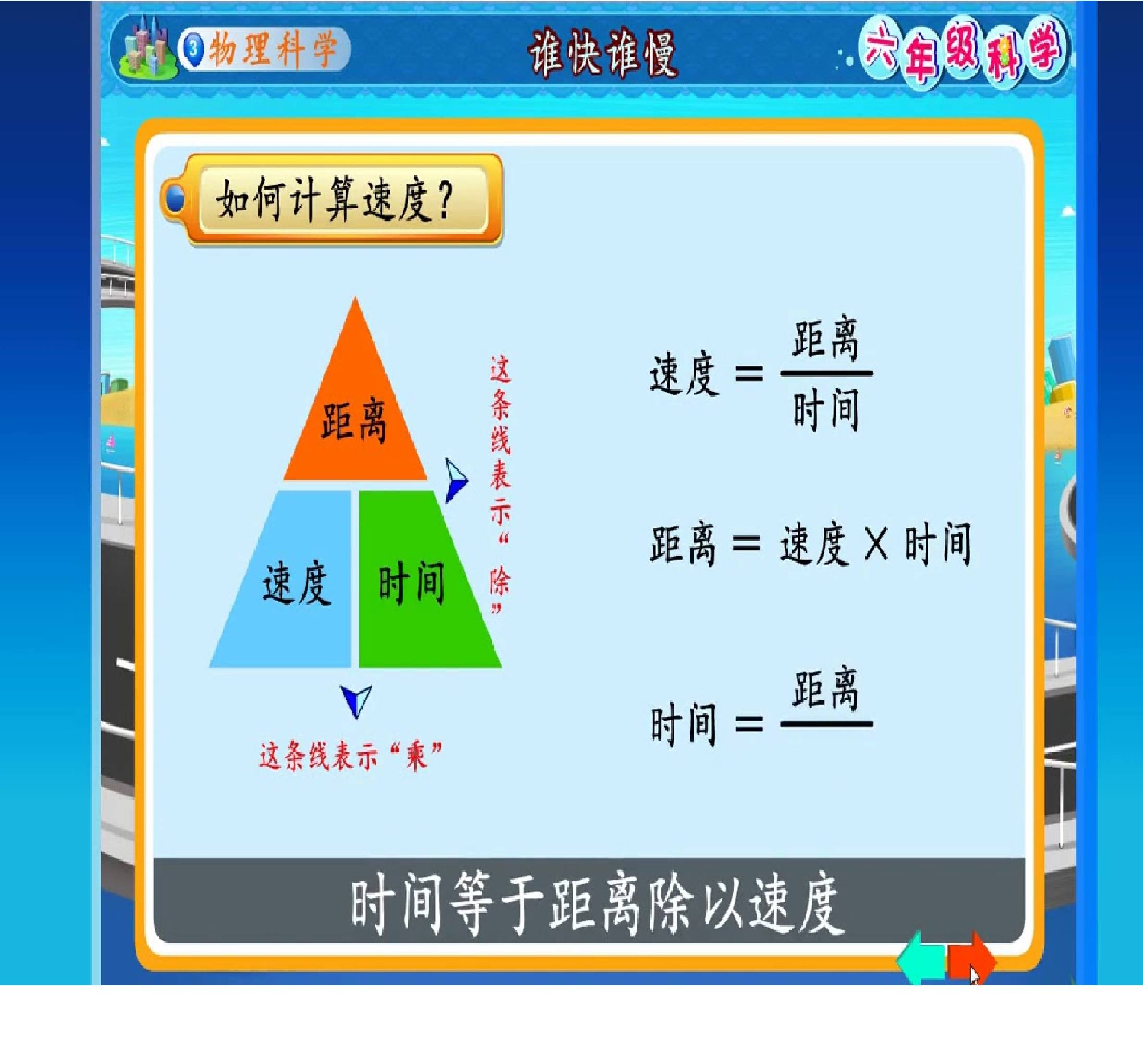
六年级科学第七课速度 Science Quiz Quizizz

怎么计算一光年 最有妙招网

如何看懂物理公式 三 以數學運算取代邏輯推理 台灣物理學會 物理雙月刊

相速度与群速度公式 简单解释 知乎

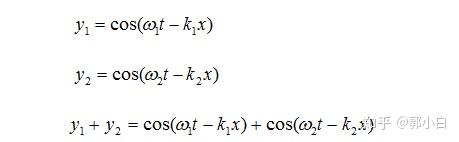
相速度与群速度公式 简单解释 知乎

直线运动

如何寻找速度 有妙招

3种方法来计算初速度

如何寻找速度 有妙招

面积公式表 新人首单立减十元 21年7月 淘宝海外

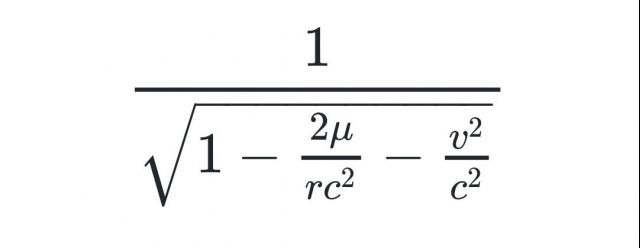
科普氵 地球和月球的时间流速差异 月球上的时间过得更快不是更慢nga玩家社区

数学行程问题公式 西瓜视频搜索

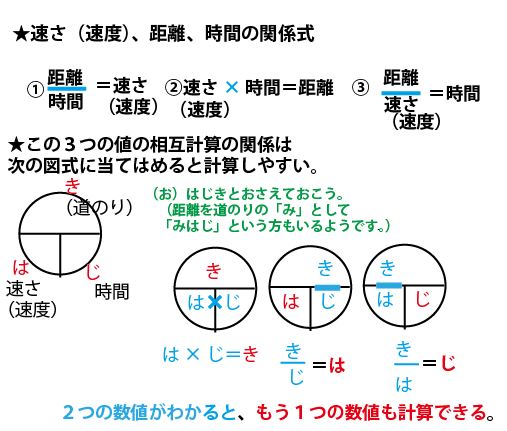
最も選択された 距離時間速度 ニスヌーピー壁紙

小学数学一到六年级计算公式汇总 Docx 文档分享网

办公高效化的跨界理解 从物理公式理解工作效率提升的路径 简书

小学生数学公式大全墙贴常用单位换算公式表知识挂图三四五六年级

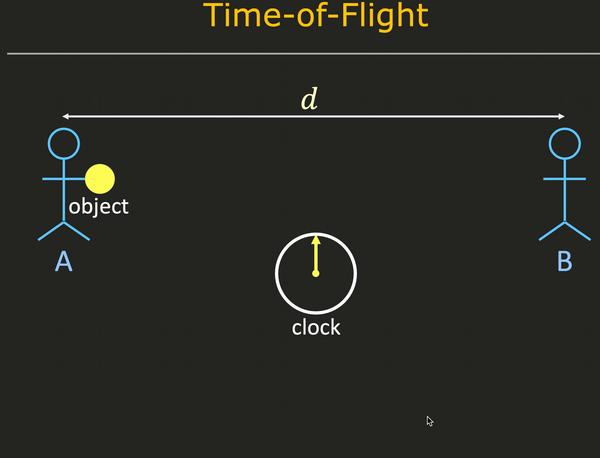
52 光的飞行时间技术 Tof系列2 知乎

愛因斯坦 預言了黑洞和大爆炸的公式 資訊咖

Q Tbn And9gcsn Wck59ccwklmoffhxmxwx2a0e8z2aytnfokfjzk6 Dyewac6 Usqp Cau

精华 人教版高中物理必修一知识点总结和练习 二 第二章匀变速直线运动 可打印 知乎

速さ 時間 距離を計算する公式の使い方と覚え方 具体例で学ぶ数学

高中物理力学复习归纳 直线运动 知乎

時間膨脹 维基百科 自由的百科全书

路程的远近 速度的快慢 时间的多久之间关系的问题称为行程问题 腾讯新闻

的公式 速度 时间 距离 如何解决这个问题呢

国考基本行程问题讲解 路程

数学两地距离的公式

行程趕路一會快一會慢 用等距平均速度公式秒解答案 雪花新闻

6年级科学 速度 Telequiz

時速公式時間 距離 速度 Rzcpe

雷达技术的基础知识 使用雷达进行距离测量

为什么当速度趋于光速时 无论多远都能瞬间到达 网易订阅

用距離速率時間公式解決問題

Q Tbn And9gcskyztyadma5wmfoihcdbbe09aev R26t Gkpp8wr5 6bos0mcc Usqp Cau

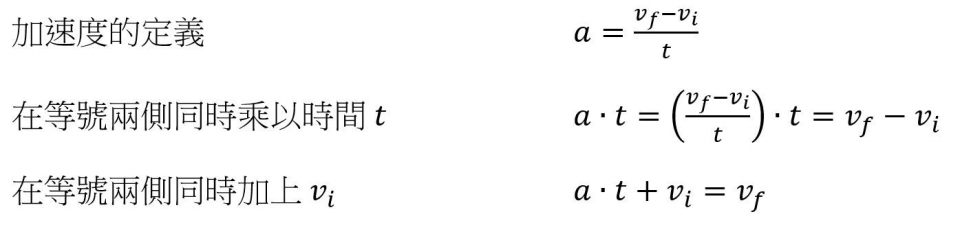
如何看懂物理公式 三 以數學運算取代邏輯推理 台灣物理學會 物理雙月刊

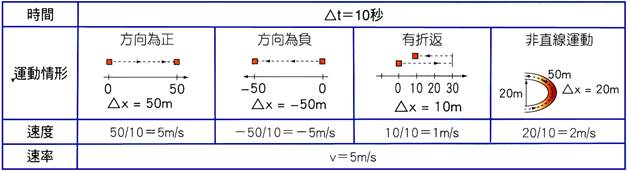
一

停課不停學 小六數學 速率 毋須死記硬背運用天平移項法推論公式 香港經濟日報 Topick 親子 親子資訊 D0303

物理时间公式 在物理中求时间速度距离的公式用字母怎么表示 三人行教育网 Www 3rxing Org

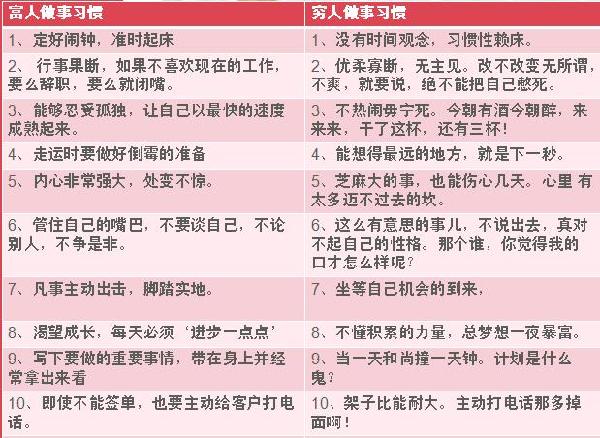
这十条做事习惯 决定你是富人还是穷人

直线运动

加速度公式距离加速度时间距离计算公式 尚书坊

距离速度时间公式 费利佩 潘通作品展 在线展览 画廊展览 雅昌展览

行程问题公式行程问题的所有公式 朵拉利品网

计算平均速度 建议 July 21

全新高中物理公式大全总结 力学公式大全第二篇

换算时间下载 换算时间格式 换算时间系统 意思 淘宝海外

加速度公式距离加速度时间距离计算公式 尚书坊

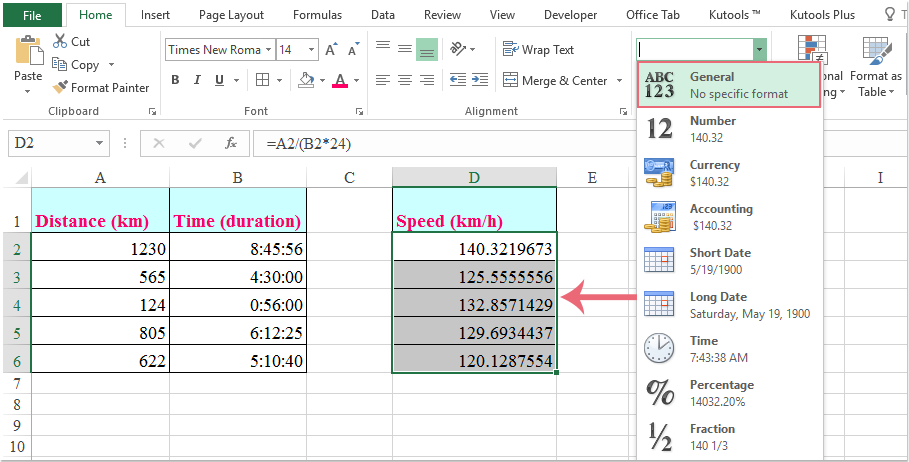
如何在excel中根據距離和時間計算平均速度

行程问题公式行程问题的所有公式 朵拉利品网

如何计算瞬时速度 包含图片

数学行程问题公式 西瓜视频搜索

1

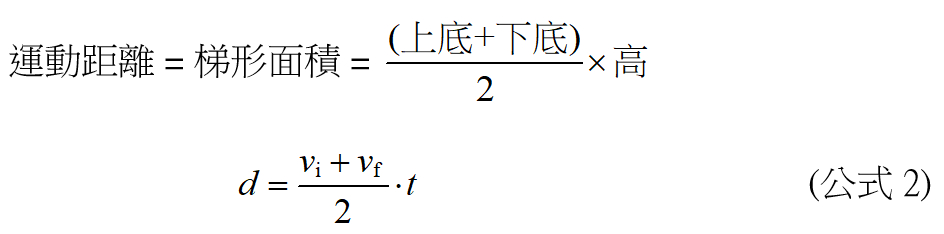
如何看懂物理公式 三 以數學運算取代邏輯推理 台灣物理學會 物理雙月刊

的公式 速度 时间 距离 如何解决这个问题呢

六年级科学 速度 Youtube

小学数学行程问题的四大解题方法及例题 每日头条

物理 点点教你怎么用公式 1 知乎

6 2 速率 時間及距離的公式 小六數學科 速率

高一高二必备 高中物理重点 考点都在这儿 6 壹读

行程趕路一會快一會慢 用等距平均速度公式秒解答案 雪花新闻

4种方法来求出速度

高等数学 速度 路程 时间公式 Qq 44的博客 Csdn博客

Facebook

速さ 時間 距離を計算する公式の使い方と覚え方 具体例で学ぶ数学

速率 10 距離 速率 時間 Youtube

3种方法来计算初速度

1

打点计时器所有公式求打点计时器的各种公式 朵拉利品网

時間膨脹 维基百科 自由的百科全书

例題 速率的單位換算1 只換距離或時間單位 數學 均一教育平台

例題 速率的三個公式應用1 速率 距離 時間 數學 均一教育平台

如何找到时间 知道距离和速度 自然科学21

如何在excel中根據距離和時間計算平均速度

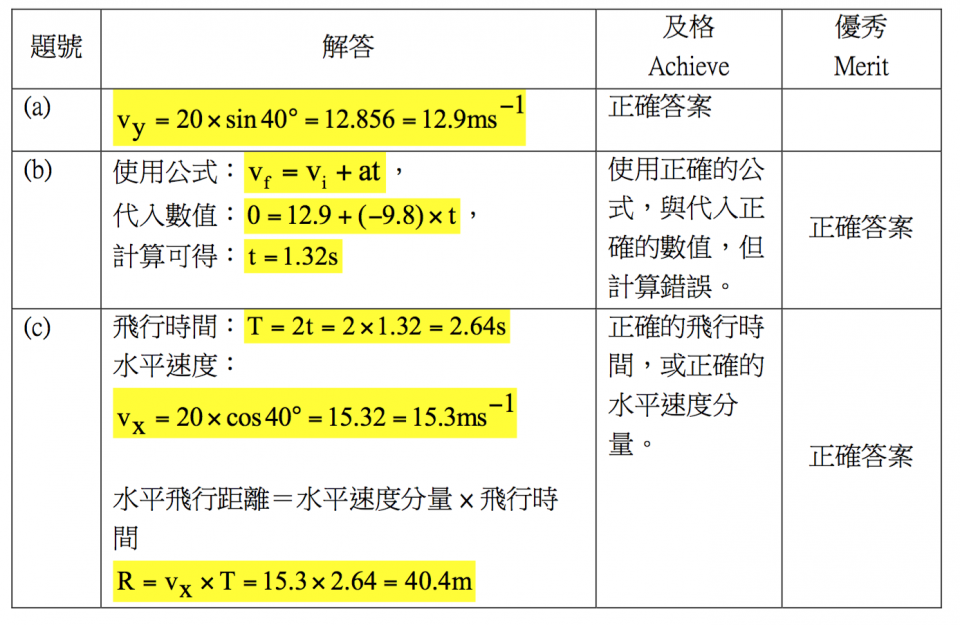
知己知彼 的教學設計 以拋體運動為例 台灣物理學會 物理雙月刊

觀念 速率公式 數學 均一教育平台

最も選択された 距離時間速度 ニスヌーピー壁紙

高等数学 速度 路程 时间公式 Qq 44的博客 Csdn博客

科学速度 Science Quiz Quizizz

速度距离时间换算公式 搜狗搜索

停課不停學 小六數學 速率 毋須死記硬背運用天平移項法推論公式 香港經濟日報 Topick 親子 親子資訊 D0303

高等数学 速度 路程 时间公式 Qq 44的博客 Csdn博客

如何看懂物理公式 三 以數學運算取代邏輯推理 台灣物理學會 物理雙月刊

一元一次方程公式 西瓜视频搜索

易学通 重难点一本过高一物理 人教版必修1 专题二匀变速直线运动的研究word版含解析下载 Word模板 爱问共享资料

Incoming Term: 距離 時間 速度 公式,