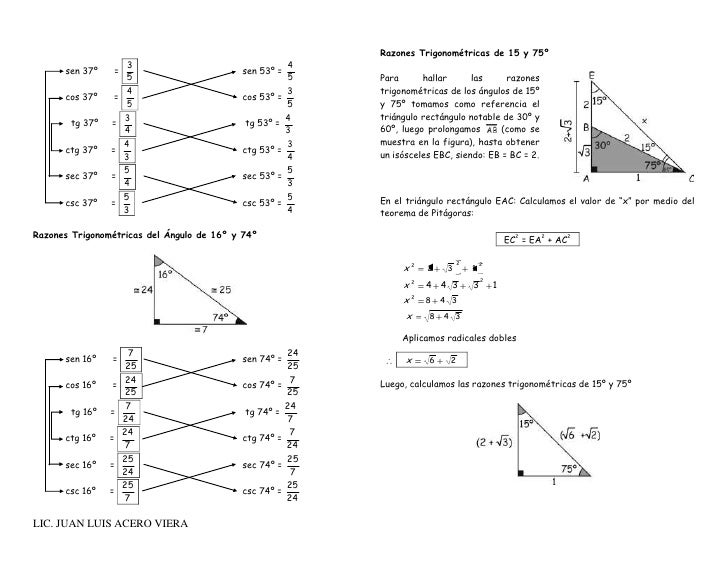
Amazoncom Royal Shade Triángulo derecho de 15 x 18 x 234 pulgadas, rojo, tamaño personalizado para hacer toldo RTAPT28, malla de toldo, triángulo de bloqueo UV, estándar comercial, resistente, 705 oz/m² Jardín y Exteriores Razones trigonométricas del ángulo mitad https//wwwyoutubecom/watch?v=0rO_CmcLgTransformando un radical doble a una suma de radicales simples https//ww √10K K 37°/2 3K El triangulo de 37/2 75° (√6 √2)K 4K √5 K K 15° (√6 √2)K El triangulo de 15 y 75 53°/2 2K El triangulo de 53/2 9 67° 5K 13K 23° 12K El triangulo de 23 y 67 50° 62° 17K K√61 8K 5K 28° 40° 6K 15K El triangulo de 40 y 50 El triangulo de 28 y 62 10

La Formula De Heron Para El Area De Un Triangulo Y Resolver Problemas Con Trigonometria Ck 12 Foundation
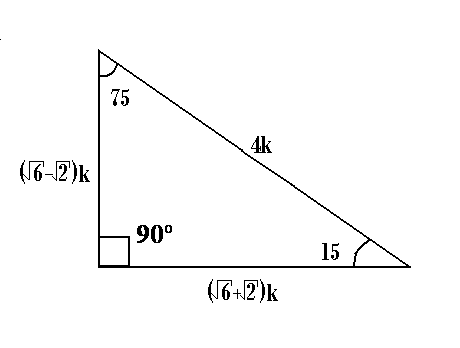
Triangulo rectangulo notable de 15 y 75 grados
Triangulo rectangulo notable de 15 y 75 grados-A 75 B 15 C 155 D 16 1 Ver respuesta adriz está esperando tu ayuda Añade tu respuesta y gana puntos eduardovillon eduardovillonUn ejemplo de un tramo de escalera que sigue la regla común pero no el código es un tramo con una unidad de distancia vertical de 875 in y una unidad de distancia vertical de 875 in El ángulo de inclinación para este tramo se obtiene por tan 1 ___ 875 875 450° Paso 3 Consulta la foto y el diagrama de la página 6 en tu libro a



Triangulo Rectangulo
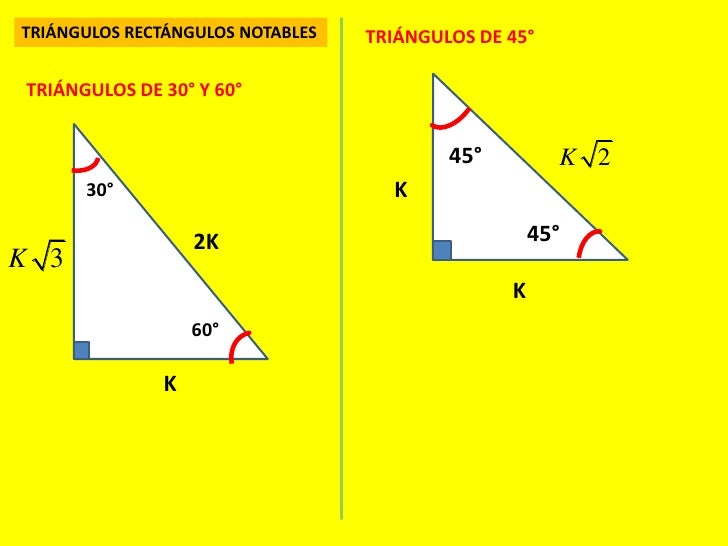
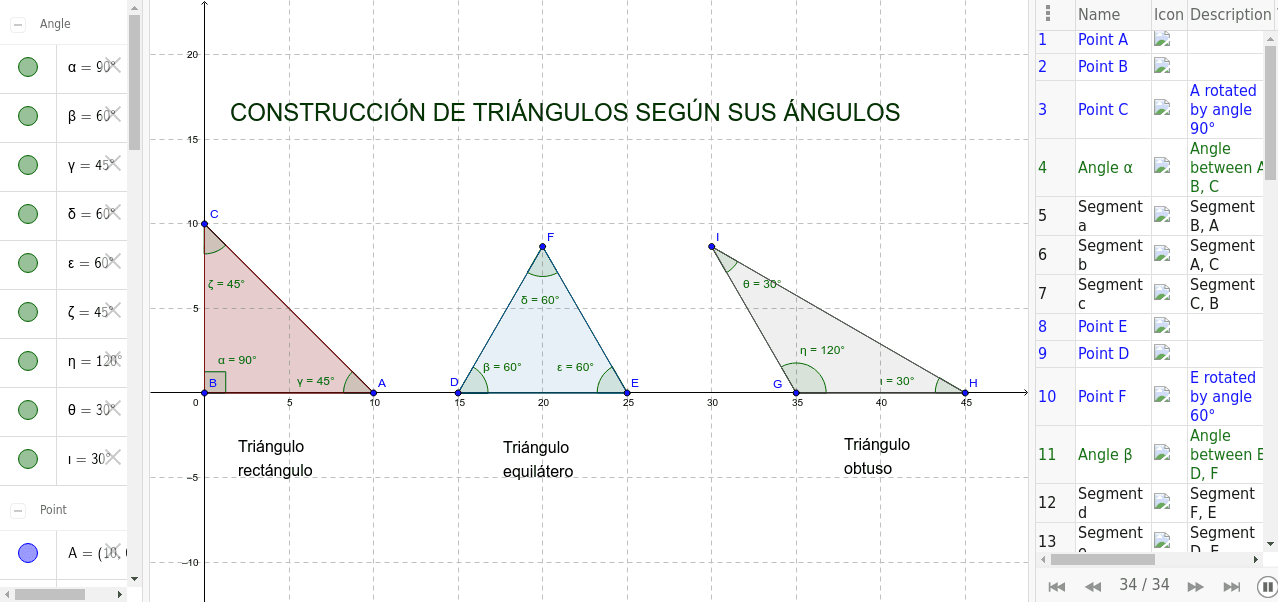
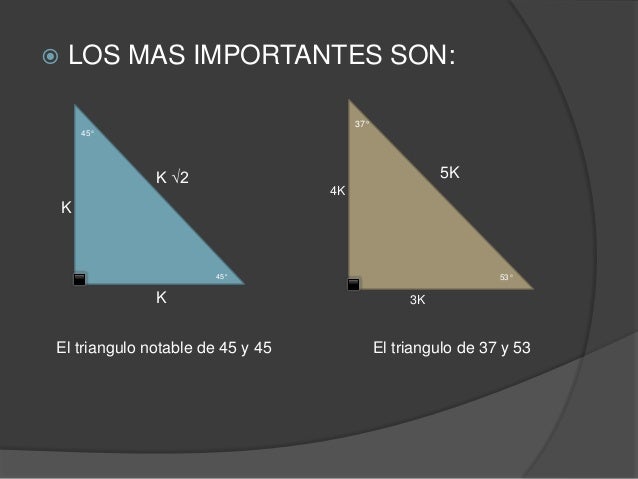
Capitulo08Trigo Triangulo Rectangulo 6 Funciones polinomiales y racionales 265 61 Funciones polinomiales 266 62 División de funciones polinomiales 275 63 Raíces y factores de funciones polinomiales 2 64 Raíces reales de funciones polinomiales 2 65 Aproximación de los ceros reales 296 66 Fracciones racionales 300 Ejercicios deEl último tipo de triángulo que vamos a aprender recibe el nombre de triángulo obtuso Un triángulo obtuso tiene un ángulo obtuso o mayor a 90 grados y dos ángulos agudos o menores a 90 grados La suma de los ángulos es igual a Ahora, es tiempo de practicar Identifica cada tipo de triángulo según sus ángulosTRIÁNGULOS RECTÁNGULOS 1) De 45° 2) De 30° y 60° 3) De 15° y 75° NOTA Existen otros aproximados, cuya relación de lados indicamos a continuación 1) De 37° y 53° 2) De 16° y 74° 3) De 56°/2 4) De 37/2 5) De 14° y 76° Borgoño Nro 409 – Trujillo / Telf 2241 16
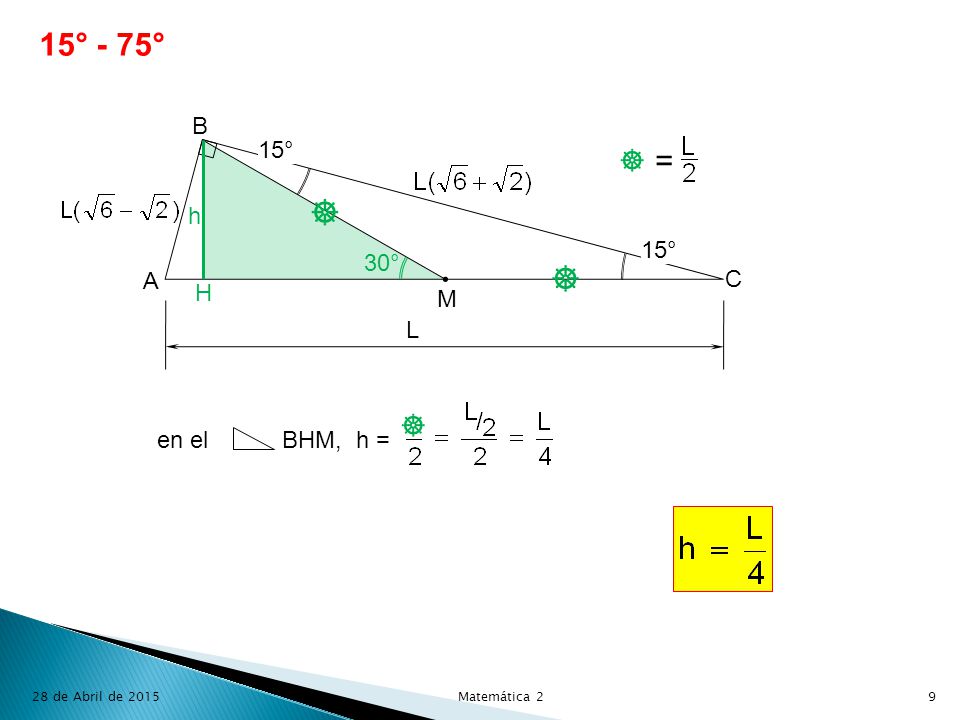
Triángulo de 30° y 75° El triángulo rectángulo de 15° y 75° este triángulo es conocido por la relación de ¼ entre altura e hipotenusa Demostración sea A, B yMatematicas Maestro Vol I Primero Grado /BLOQUE II/SECUENCIA Multiplicación números decimales Pág 1Mathematics, 1530, LadyHolmes67 When i add money am i supposed to make it like this 712 or because i got 19 dollars for my answer Answers 2
ADMISIÓN 112 CON GRUENCIA DE TRIÁNGULOSAnswers Answer from shygirltn 105° Stepbystep explanation 9015 75 15 Answer from Quest Answer v= lwhstep by step explanation length x width x heightl = 12kmw = 6kmh = 6km12 x 6 = 7272 x 6 = 432therefore your answer wouldDe 30 y 60 grados El triángulo notable de 30 y 60 (treinta y sesenta), este triángulo presenta una longitud de hipotenusa que es el doble del tamaño del cateto menor del triángulo De 15 y 75grados El triángulo notable de 15 y 75 es otro clásico que se suele presentar en repetidas ocasiones dentro de los problemas matemáticos




Problema 434



Triangulos Ii Dibujo Tecnico 2º Bachillerato
Triángulos rectángulos notables (propiedades) si los ángulos agudos de un triángulo rectángulo son de 15 y 75 La altura correspondiente a la hipotenusa es igual a la cuarta parte de ella Nota proporciones y semejanzas En un triángulo rectángulo, con esas medidas, según el Teorema de Pitágoras, la hipotenusa H es tal que H² = (15 cms)² (8 cms)² H² = 225 cms² 64 cms² H² = 2 cms² H = √ (2 cms²) H = 17 cms Los ángulos agudos A y B son tales que Sen A = 15 cms / 17 cms Sen A = 0, 52 A = Arc Sen(0, 52) En el triángulo isósceles de base BC, los ángulos que se oponen a los lados congruentes miden cada uno 15°, en consecuencia el triángulo rectángulo ABC, tiene medidas de 15° y 75




La Formula De Heron Para El Area De Un Triangulo Y Resolver Problemas Con Trigonometria Ck 12 Foundation




Triangulos Notables Ejercicios Resueltos Pdf
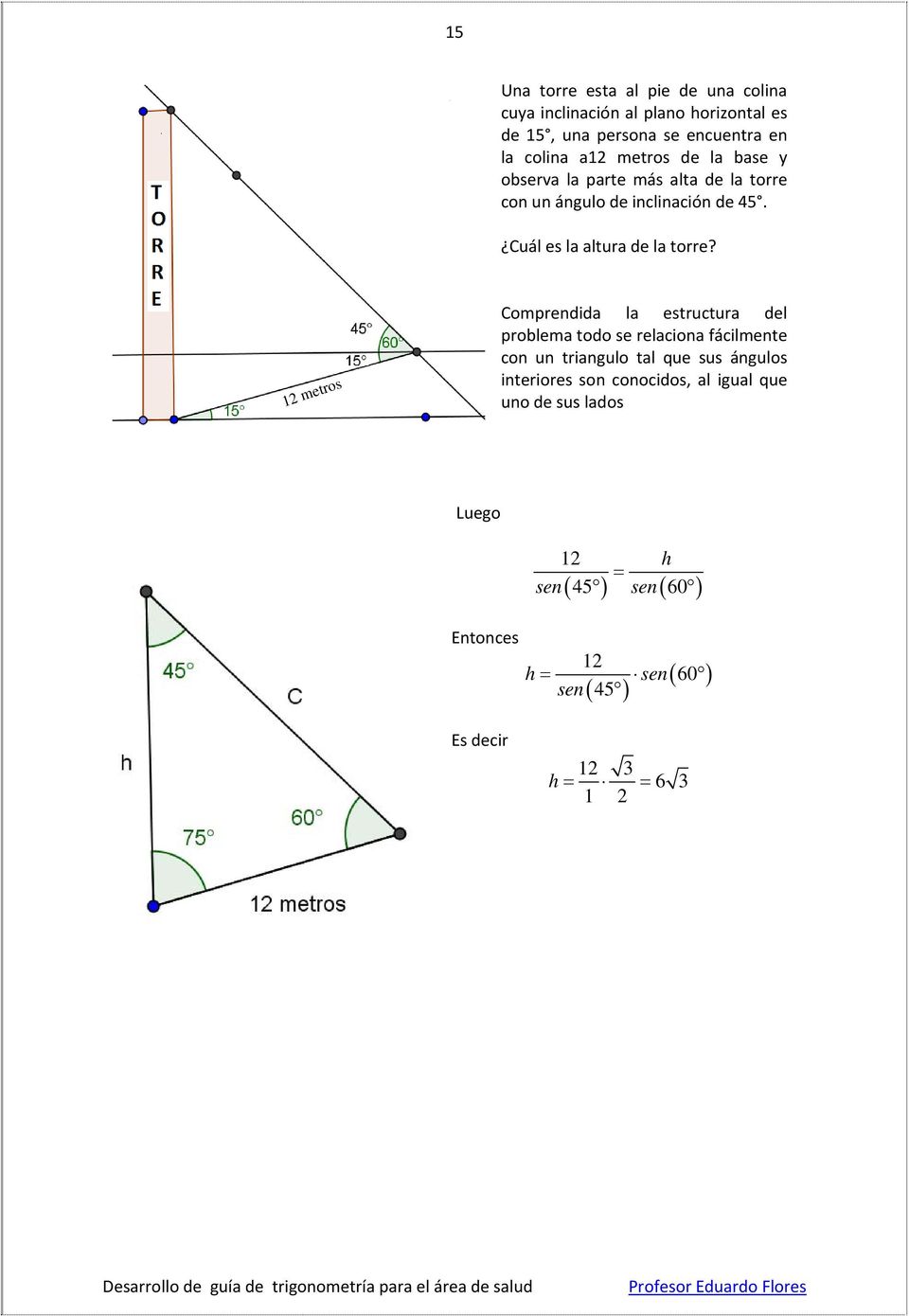
Un palo vertical de 1,75 m proyecta una sombra de 2 mSi la sombra de un edificio el mismo día,en el mismo sitio y a la misma hora mide 24 m,¿cuánto mide de alto el edificio?La superficie de una esfera es de 15 m2 Halla la superficie de otra esfera en la que el radio mide el triple Solución S' = 32 15 = 135 m2 7 Solución 224El área de un triángulo es base ( b b) por altura ( a a) divido entre 2 Como sabemos que el área es 15 c m 2 15 c m 2 y que la base es b = 6 c m b = 6 c m, podemos calcular la altura La altura del triángulo es 5cm Finalmente, calculamos la hipotenusa aplicando Pitágoras La hipotenusa mide, aproximadamente, 781cm




Triangulo Notable De 15 Y 75 6 Youtube



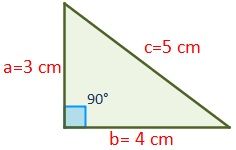
Los Catetos De Un Triangulo Rectangulo Miden 3 Cm Y 4 Cm Respectivamente Cuanto Mide El Coseno Del Menor Angulo 3 Sin A 5 4 Cos A Pdf Descargar Libre
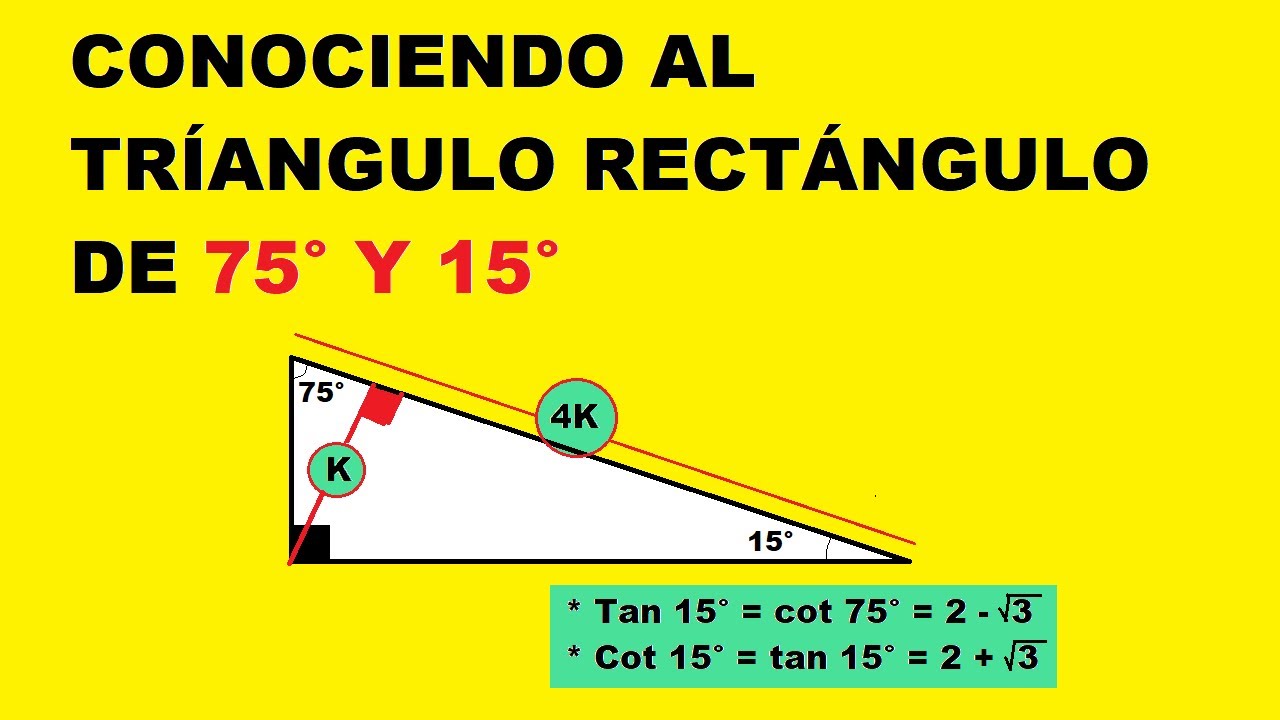
Triángulo rectángulo de 15 y 75 grados, ayuda como lo resuelvo 1 Ver respuesta anyelo está esperando tu ayuda Añade tu respuesta y gana puntos fernandomontenegro19 fernandomontenegro19Razones trigonométricas de los ángulos de 75° y 15° 6 2 sen15 cos75 4 tan15 2 3 cot75 sec15 6 2 csc15 3 ÁREA DE UNA REGIÓN TRIANGULAR 31 Área en función de dos lados y el ángulo comprendido Determinando una altura del triángulo ABC Si h senC b , entonces h bsenC luego, absenC S 2 es el área de la región triangular ABC 32 ÁreaHola alguien sabe como resolver un ejercicio de un triángulo rectángulo de 15 y 75 grados?




Resolucion De Triangulos Matematicas Ies




Puntos Y Rectas Notables Del Triangulo Matematicascercanas
1 Ver respuesta anyelo está esperando tu ayuda Añade tu respuesta y gana puntos fernandomontenegro19 fernandomontenegro19 Respuesta X TRIANGULO RECTANGULO Teorema de Pitágoras "La suma de cuadrados de los catetos es igual al cuadrado de la hipotenusa" a2 b2 = c2 Teorema "Los ángulos agudos de un triángulo rectángulo son complementarios" 2 y2 =172 64y2 =2 y2 =225 y= 15 Como "y" esta en el tercer cuadrante entonces tiene que ser negativo y=15 6Utilizando 0,26 como valor aproximado para a tangente de 15° e duas casas decimais nas operações, descobrese que a área da base desse prédio ocupa na avenida um espaço a) menor que 100 m 2 b) entre 100 m 2 e 300 m 2 c) entre 300 m 2 e 500 m 2 d) entre 500 m 2 e 700 m 2




Triangulos Rectangulos Notables




Resolucion De Triangulos Superprof
TRIÁNGULO RECTÁNGULO NOTABLE DE 15° Y 75° TRIÁNGULOS RECTÁNGULOS ( de medidas de ángulos agudos aproximados) DE 37° Y 53° DE 53°/2 DE 37°/ a√ 2 45° a a 45° a a a√ 3 60° 30° 37 °/2 3a a 37° 53° 3k 4k 5k h = a 53°/2 2b b 15° h 4a El área de un rectángulo mide 15 unidades cuadradas Si un lado del rectángulo mide 375 unidades de largo, ¿cuántas unidades mide el perímetro del rectángulo? Luego de haber hecho esto, la mayoría querría usar el Triángulo Rectángulo Notable de 15° y 75° pero seria muy tedioso ya que sus lados contienen raíces proporcionales Así que en vez de eso, expandiremos el lado BC de manera que el lado AB sea igual a la expansión ( lado CP )




Perimetro De Un Triangulo Rectangulo



Triangulos Problemas
Respuestamide 75 cmExplicación paso a pasola área de un triángulo es base por altura dividido entre dos10x15 = 75 2La fórmula de Herón da para el área S= √p(pa)(pb)(pc) → S=√(21*8*7*6)=√(3*7*2³*7*2*3)=√(2⁴*3²*7²)=2²*3*7=84Ejercicios Calcular el valor de la hipotenusa o el cateto según sea el caso a




Todo Los Triangulos Notables Sus Angulos Medidas




Teorema De La Suma De Un Triangulo Ck 12 Foundation
Si El centro del círculo estará en el punto medio de la hipotenusa (que resulta ser un diámetro) y el tercer vértice está en un arco capaz de 90 grados (para que el triángulo sea rectángulo) que será un lugar geometrico que será la circunferencia con centro en el punto medio de la hipotenusa y que pasa por sus extremos Triángulo Notable de 15° y 75° If playback doesn't begin shortly, try restarting your device An error occurred while retrieving sharing information Please try again laterVeja grátis o arquivo Trigonometria Teoría y Prática enviado para a disciplina de Trigonometria Categoria Exercício 14



Trigonometria 1ra Parte



Www Uv Es Lonjedo Esoproblemas 3eso14triangulo Pdf
Uno de los ángulos de un triángulo rectángulo mide 15° ¿Cuánto mide el otro ángulo agudo? Lo bueno, malo y feo de la capacitación a directores Jesus Mendez Leer Teoría Triángulo Notable de 15° y 75° previous Razones trigonométricas de ángulos notables Parte II next Triángulo Notable de 37°/2 y 53°/2Triangulos rectangulos notables de 75 y 15 Triangulos rectangulos notables de 75 y 15




Triangulo Notable De 15 Y 75 Profesorajesus Com




La Medida De Uno De Los Angulos Agudos De Un Triangulo Rectangulo Es El Quintuplo Del Otro Halla La Brainly Lat
teniendo en cuenta sus propiedades y proporciones resolveremos problemas respecto a este triangulo notableAbout Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us CreatorsRespuesta a la pregunta Los tres lados de un triangulo mide 13 cm 14 cm 15 cm el triangulo es rectangulo solucioneslatcom



Www Cbtis136 Edu Mx Public Noticias D167e3c6b532f70ac4f18db11a6a4e90 Pdf




Trigonometria Problemas De Matematicas Resueltos
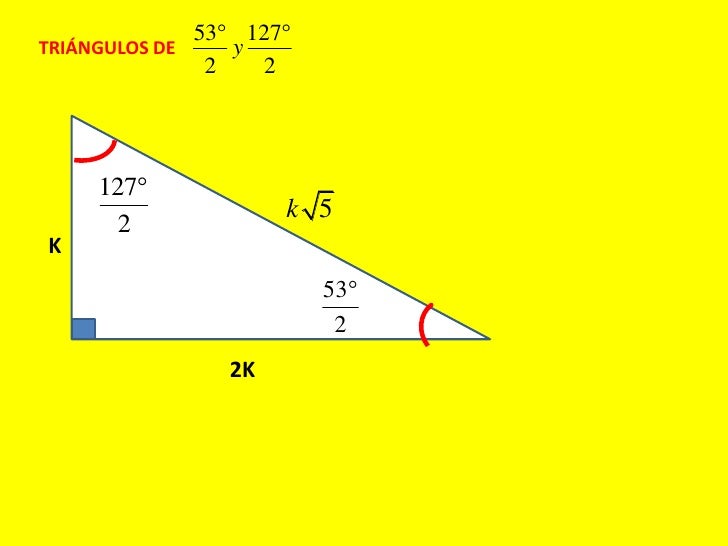
Un triángulo 30°60°90° es comúnmente encontrado como un triángulo rectángulo cuyos lados están en la proporción Las medidas de los lados son x , , y 2 x En un triángulo 30°60°90°, la longitud de la hipotenusa es dos veces la longitud del cateto más corto, y la longitud del cateto más largo es veces la longitud del cateto{26, 28, 30} Podemos dividir por el MCD igualmente, sin que el triángulo deje de ser herónico, y nos sale nada menos que el triángulo de Herón {13 , 14 , 15} El semiperímetro será p =()/2=21;3 Triángulos rectángulos notables exactos 31 Triángulo de 45° 32 Triángulo de 30° y 60° 33 Triángulo de 15° y 75° 34 Triángulo de 36° y 54° 35 Triángulo de 22°30′ 4 Triángulos rectángulos notables aproximados 41 Triángulo de 37° y 53° 42 Triángulo de 16° y 74°




Pin En Trigonometria Yuma




4 Dos Lados De Un Triangulo Rectangulo Miden 8cm Y 15 Cm Calcula Cuanto Mide La Hipotenusa Y Halla Brainly Lat
9 15 0,75 12== Ejercicio nº 12 Calcula la altura de un árbol que proyecta una sombra de 12 metros en el momento en que otro árbol que mide 2,5 m proyecta una sombra de 4 metros Solución Un rectángulo tiene unas dimensiones de 15 cmY ahora viene la observación buena de David en su respuesta, si nos dan como dato que la hipotenusa vale 10 y el perímetro vale 24 resulta que es un triángulo semejante al anterior en que los lados se han multiplicado por un factor de 2 y por tanto las longitudes de los otros catetos resultan ser 6 y 8De 30 y 60 grados El triángulo notable de 30 y 60 (treinta y sesenta), este triángulo presenta una longitud de hipotenusa que es el doble del tamaño del cateto menor del triángulo De 15 y 75grados El triángulo notable de 15 y 75 es otro clásico que se suele presentar en repetidas ocasiones dentro de los problemas matemáticos




Triangulo Rectangulo De 75 Y 15 Youtube




Todo Los Triangulos Notables Sus Angulos Medidas
En los triángulo notable existe una relación conocida entre sus lados y ángulos Los triángulos notables son de 37°, 53°, 45°, 74°,76°, 30°, 60° entre otrosMichael Jordan mide 210 m de estatura, si se encuentra en la Alameda Central, y en ese momento la proyección de su sombra es de 375 m, ¿cuál es la distancia de su sombra?Trigonometría y Triángulos Rectángulos Objetivos de Aprendizaje Usar el Teorema de Pitágoras para encontrar las longitudes desconocidas de los lados de un triángulo rectángulo Encontrar las longitudes y ángulos desconocidos de un triángulo rectángulo Encontrar los valores exactos de una función trigonométrica para ángulos que miden 30°, 45°, y 60°




Triangulo Rectangulo Problema 7 Basico




Teorema De La Suma De Un Triangulo Ck 12 Foundation
El triángulo notable de 30 y 60 (treinta y sesenta), este triángulo presenta una longitud de hipotenusa que es el doble del tamaño del cateto menor del triángulo De 15 y 75grados El triángulo notable de 15 y 75 es otro clásico que se suele presentar en repetidas ocasiones dentro de los problemas matemáticos De 16 y 74 grados Para más ejercicios resueltos de triángulos notables y de matemática, visita totalmente gratis los siguientes enlaceshttp//mihijoconbuenanotaenmatecom/ht




Ideas De Trigonometria Trigonometria Razones Trigonometricas Secundaria Matematicas



Triangulo Rectangulo



Construccion De Triangulos Segun Sus Angulos Geogebra




Mates 1ºeso Avanza Santillana By Eduardo Mena Issuu



Www Matematicasonline Es Segundoeso Ejercicios Pitagoras Cuadernillo Pdf



1



Unidad Vii Geometria Trigonometria Y Series



Http Www Prepa5 Unam Mx Wwwp5 Profesor Publicacionmate 05ii Pdf



3




Incentro De Un Triangulo




Solucionador Automatico De Problemas De Geometria El Triangulo




Paginas Desdetrigonometria 5 Act Triangulo Geometria Clasica



Http Www Edu Xunta Gal Centros Iesortigueira System Files 2eso matem C3 81ticas semana 5 Pdf



Deducir Los Senos Y Los Cosenos



Solucionador Automatico De Problemas De Geometria El Triangulo



Triangulos Notables
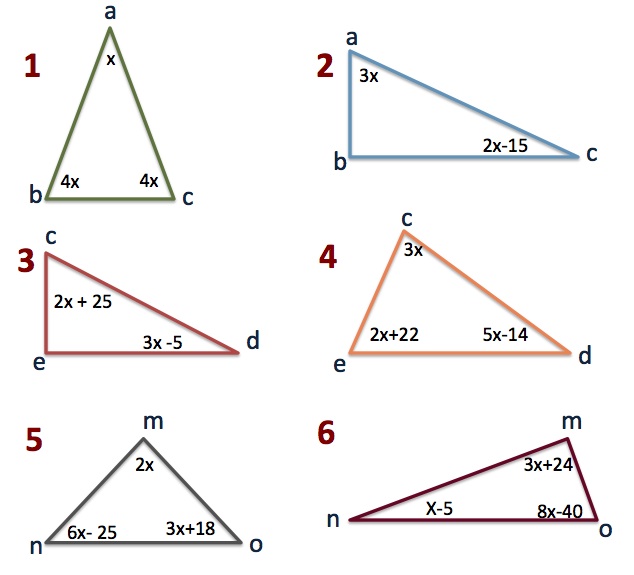



Algebra Triangulos Y Ecuaciones Spanish Ged 365



Solucionador Automatico De Problemas De Geometria El Triangulo
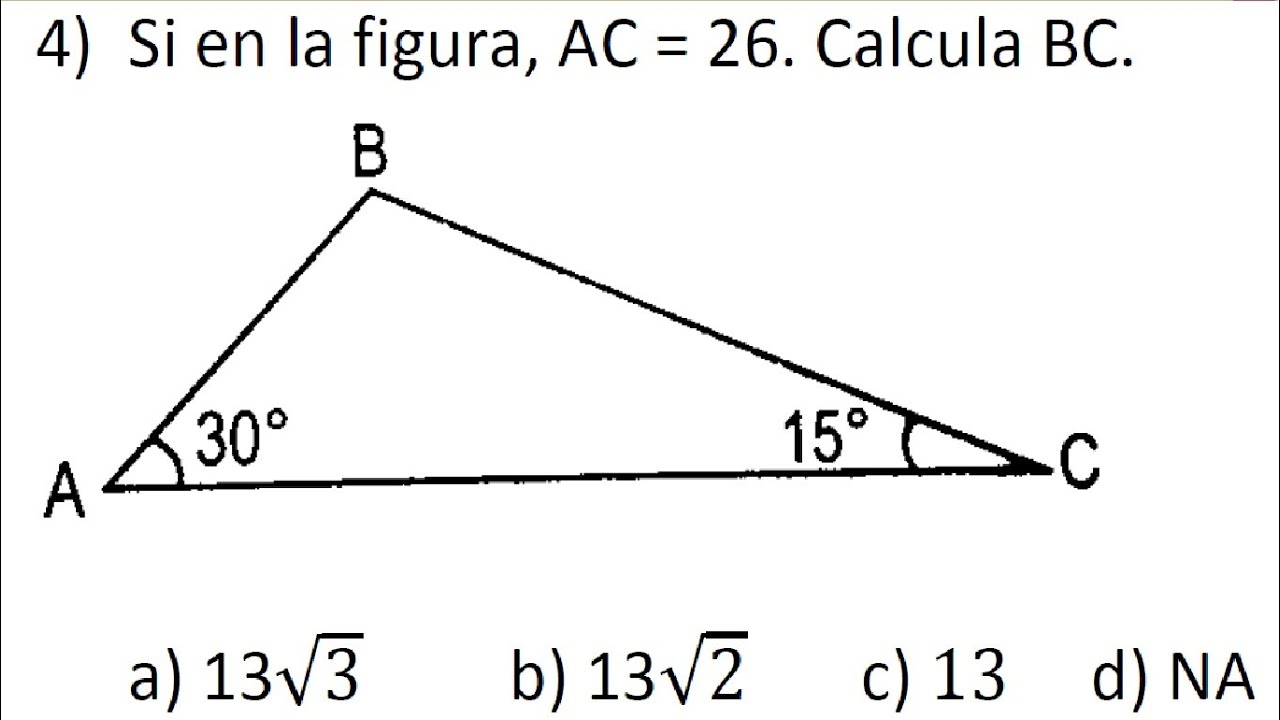



Triangulo Rectangulo Notable 15 Y 75 Youtube








Todo Los Triangulos Notables Sus Angulos Medidas



Resolucion De Triangulos



Www Cbtis136 Edu Mx Public Noticias D167e3c6b532f70ac4f18db11a6a4e90 Pdf




Triangulos Rectangulos Notables Matemath



Www Matematicasonline Es Cuarto Eso Repaso3 6 Trigonometria Aplicaciones Pdf




Triangulo Isosceles




4 Resolver Triangulos



Matematica 2 Epe Area De Ciencias Ma De Abril De Ppt Descargar




Todo Los Triangulos Notables Sus Angulos Medidas



Perimetro De Un Triangulo Rectangulo




Triangulos Rectangulos Notables Matemath




Triangulo Rectangulo Notable De 15 Y 75 Youtube



Archivo Triangulo Auxiliar De 75 Y 15 Png Wikipedia La Enciclopedia Libre



1




H1jv7nihts2d M



Www Cbtis136 Edu Mx Public Noticias D167e3c6b532f70ac4f18db11a6a4e90 Pdf




Triangulos Notables Wikipedia La Enciclopedia Libre




Triangulos Geometria Ejercicios Docsity




Trigonometria




Pagina 172 Pag 1 Unidad 8 Teorema De Pitagoras Semejanza Pdf Descargar Libre




Razones Trigonometricas Ppt Video Online Descargar



Un Interesante Triangulo Notable 75 Y 15 Conclusiones Youtube




Informatica 15 Aula Verde Matematicas



Deducir Los Senos Y Los Cosenos



Teorema De Pitagoras Mathematics Quizizz



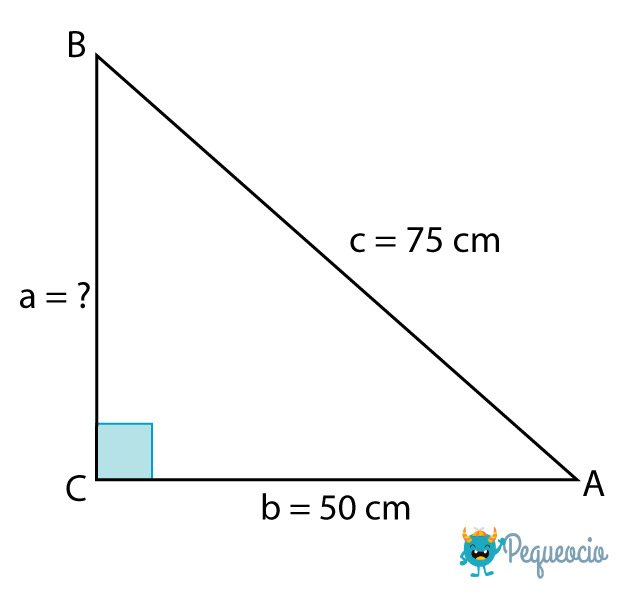
Perimetro De Un Triangulo Rectangulo



Resources Aprendoencasa Pe Perueduca Secundaria 5 Semana 14 Pdf S14 Sec 5 Solucion Matematica Dia 3 Pdf




Triangulo Rectangulo




Todo Los Triangulos Notables Sus Angulos Medidas




Resolucion De Triangulos Superprof




Bloque Ppt Descargar



Www Uv Es Lonjedo Esoproblemas 3eso14triangulo Pdf




En Un Triangulo Rectangulo La Cotangente De Uno De Sus Angulos Agudos Es 0 75 Calcular La Brainly Lat




Triangulos Notables 15 75




Triangulos Notables De 15




Triangulos Notables Estudiandoenlinea




La Hipotenusa De Un Triangulo Rectangulo Mide 35 Cm Y El Angulo Agudo B 43 15 Calcular Los Brainly Lat



Mestreacasa Gva Es C Document Library Get File Folderid Name Dlfe 2677 Pdf




Ejercicio De Triangulo Rectangulo



Deducciones Del Teorema De Pitagoras A Lo Largo De La Historia Como Recurso Didactico En El Proceso De Ensenanza Aprendizaje De La Matematica




Perimetro De Un Triangulo Rectangulo




Triangulos Rectangulos Notables Matemath



Unidad Vii Geometria Trigonometria Y Series




Triangulos De 30 Y 60 45 Y 45 37 Y 53 Razones Trigonometricas Notables Ejercicios Resueltos Pdf




Ejercicios Con Triangulos Oblicuangulos Superprof




Todo Los Triangulos Notables Sus Angulos Medidas



Verso Mat Uam Es Web Index Php Documentos Category 18 Premio V 10 11 Download 162 Triangulos Progresiones




H1jv7nihts2d M




Resolucion De Triangulos Superprof



3
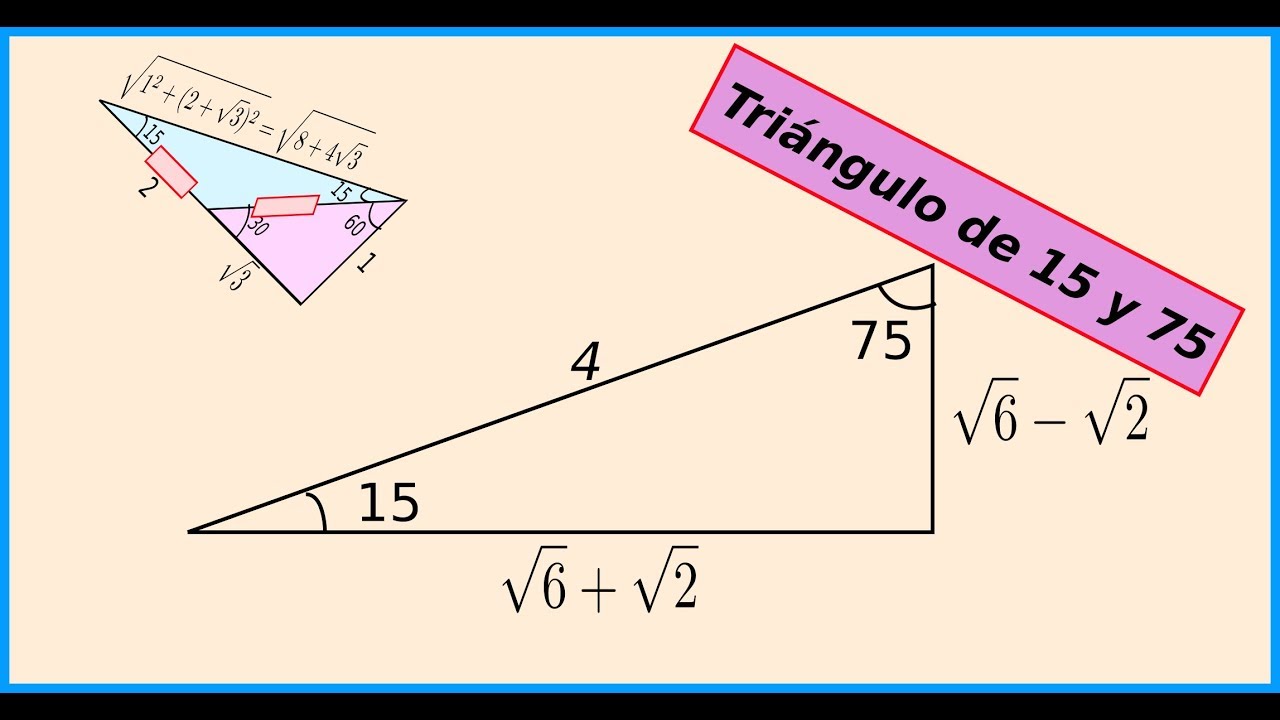



El Triangulo De 15 Y 75 Grados Youtube




Todo Los Triangulos Notables Sus Angulos Medidas
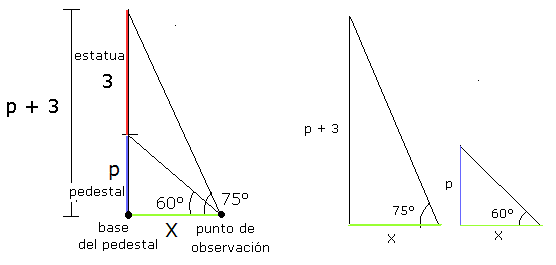



Triangulos Rectangulos Y Oblicuangulos Matematica Y Listo Respuestas
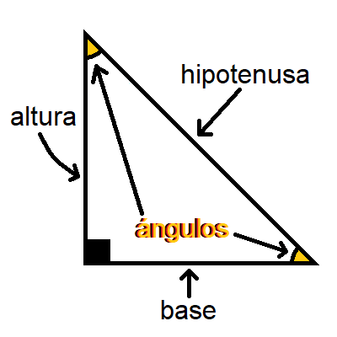



Triangulos Notables Wikipedia La Enciclopedia Libre




Triangulos Rectangulos Notables Matemath




Hola Alguien Sabe Como Resolver Un Ejercicio De Un Triangulo Rectangulo De 15 Y 75 Grados Brainly Lat
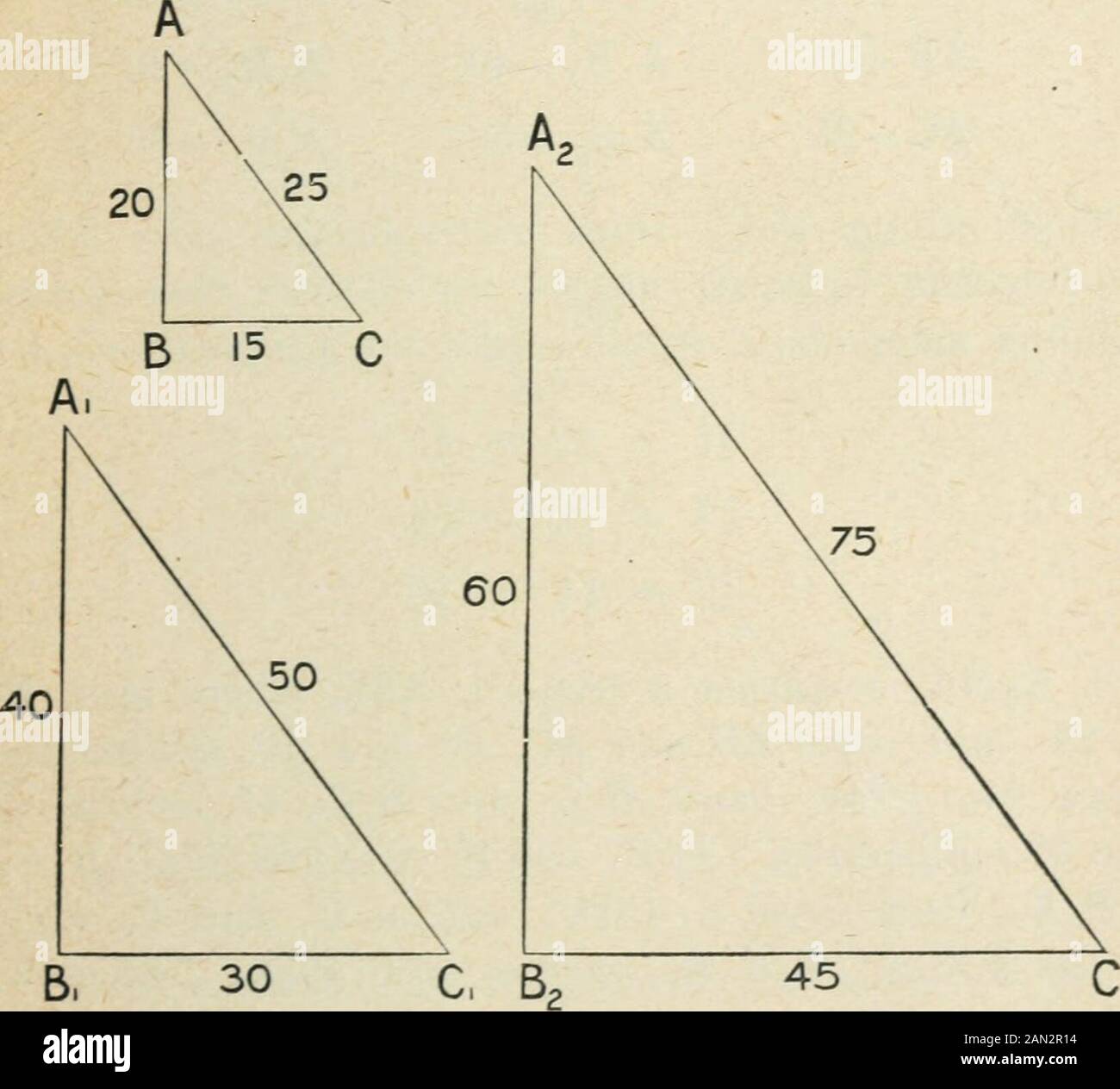



Geometria Del Plano Elemental Inductivo Y Deductivo Por Alfred Baker Hexagono Egular Mostrar Que Su Area Es Twicela Del Triangulo Equilatero Ace 19 En Un Circulo El Angulo Abc




Triangulo Notable De 15º Y 75º Demostracion Youtube



0 件のコメント:
コメントを投稿