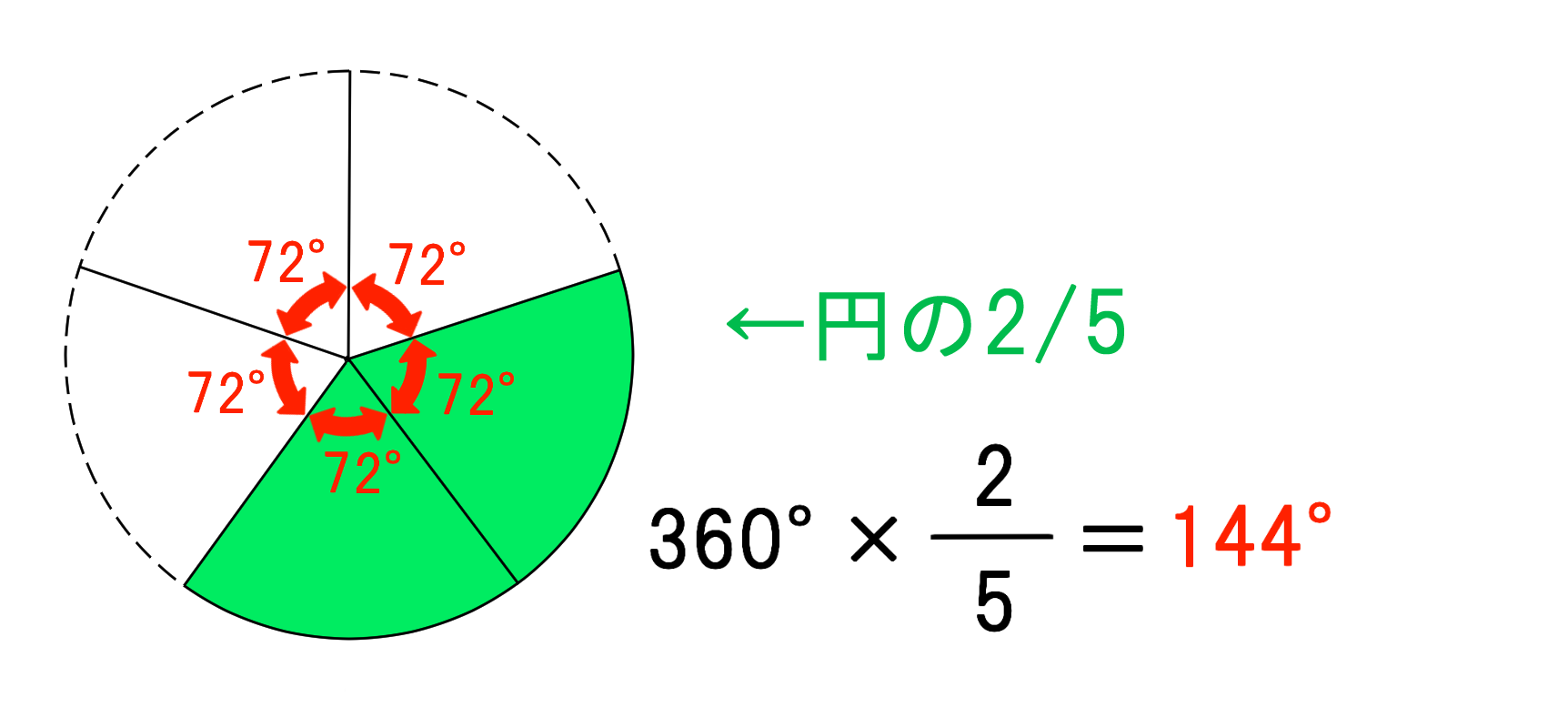
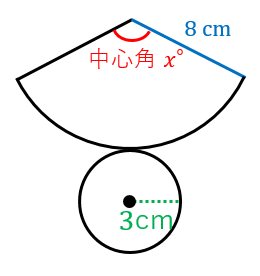
おうぎ形の中心角の求め方 中心角=(おうぎ形の面積/円の面積)×360 中心角=(おうぎ形の弧の長さ/円周)×360 例題3 おうぎ形の面積を求める公式は \ おうぎ形の面積 = 円の面積 \times \frac{中心角}{360°} \ なので、円の半径を \(r\) とするとおうぎ形の中心角を求める問題で,わかっている数字が変わると求め方がわからなくなります。 底面の半径が3cmなので、円周=直径× π =6 πcm となります。 底面の円周とおうぎ形の孤の長さは等しいので、孤の長さも6 π cmです。 そこから、半径12cm&孤の長さ6 π cmのおうぎ形の中心角を逆算して求める──これが一般的な解き方です。

扇形の公式は暗記しない 割合という考え方を導入するだけでスラスラ解ける 中学受験ナビ
おうぎ形 中心角 求め方 面積
おうぎ形 中心角 求め方 面積- ベストアンサー:半径=√{中心角×面積/(360π)} です。 例えば、中心角60°、面積24πなら 半径=√{60×24π/(360π)}=√4=2 のように求められる。 おうぎ数学1 平面図形 円とおうぎ形半径と弧の長さ,半径と面積から おうぎ形の中心角を求める。 https//math7daifukublogspotjp/




扇 おうぎ 形の面積を求める公式と弧の長さの求め方
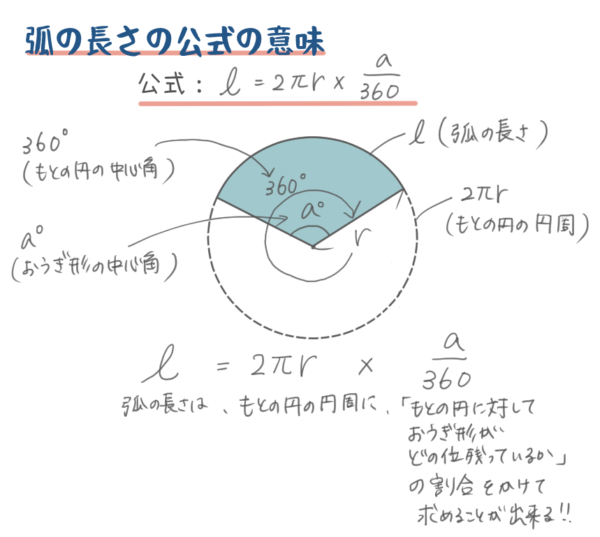
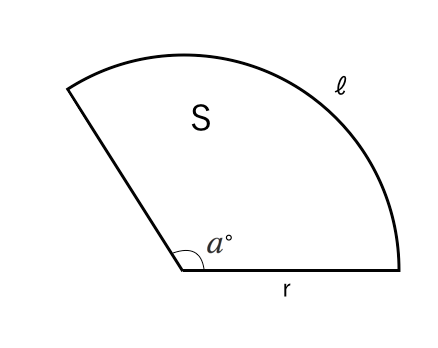
おうぎ形の面積 = 円の面積 × 中心角 360° 中 心 角 360 ° = 半径×半径×314 × 中心角 360° 中 心 角 360 ° 今回の中1数学の解説は「おうぎ形の中心角の求め方」についてです。 弧の長さや面積が与えられている時どのようにして中心角を求めるのかを確認していきましょう。 hissoritophysmathcom 今回は ・円錐の中心角の求め方 についてです。 弧の長おうぎ形の弧の長さや面積は中心角に比例するので, おうぎ形の弧の長さや,面積を求めるには, 円周の長さや,円の面積に 中心角 360° をかければよい。 半径rで中心角がaのおうぎ形 弧の長さ l = 2πr × a 360 面積 S = πr2 × a 360 例半径18cm, 中心角40°の
おうぎ形弧の長さ・面積・中心角の求め方 21年2月1日 学習内容解説ブログサービスリニューアル・受験情報サイト開設のお知らせ 学習内容解説ブログをご利用下さりありがとう 既に知ってる「扇の中心角を求める問題」に変えてしまう っていうのがポイント! 扇の中心角の求め方を知らない人は、 扇形の中心角の求め方3パターンを見てみてね ちなみに、中心角を求める公式もあって $中心角 = 360 \times \dfrac{半径}{母線}$以下のおうぎ形について中心角を求めなさい。(ただし円周率は314とします。) (1)半径10cmで弧の長さが157cm 基本的な解き方 「半径が等しいおうぎ形のポイント」を利用した解き方 360×157/628=90 答え 90 ° 工夫した解き方
中心角を \(x\) とすると、扇形の面積公式を利用し $$\pi \times 6^2\times \frac{x}{360}=12\pi$$ という方程式を作ることができます。 あとは、この方程式を解いていくだけです。 $$\frac{x}{10}=12$$ $$\frac{x}{10}\times 10=12\times 10$$ $$x=1°$$ よって、扇形の中心角は1°となります。 この2つさえ覚えていれば、中心角を求めるだけじゃなくて 面積や弧の長さを求める問題にも対応できるようになるよ じゃあ、具体的に見ていこうね 具体的に解く 中心角の求め方の問題は3パターン考えられるよ 弧の長さと半径が分かっている場合 5 おうぎ形の中心角の出し方 6 四角形の4辺の長さと対角線のなす角がわかっている時、対角線の長さを求める方法を教えていただけますか。 7 図のように正六角形をその中心で通る対角線で区切り、6個の合同な正三角形に分ける。




高校入試対策数学 円錐に関する対策問題 Pikuu




おうぎ形の面積 弧の長さ 数学ノート
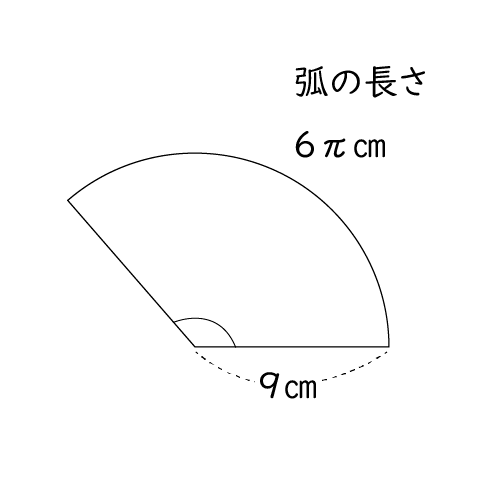
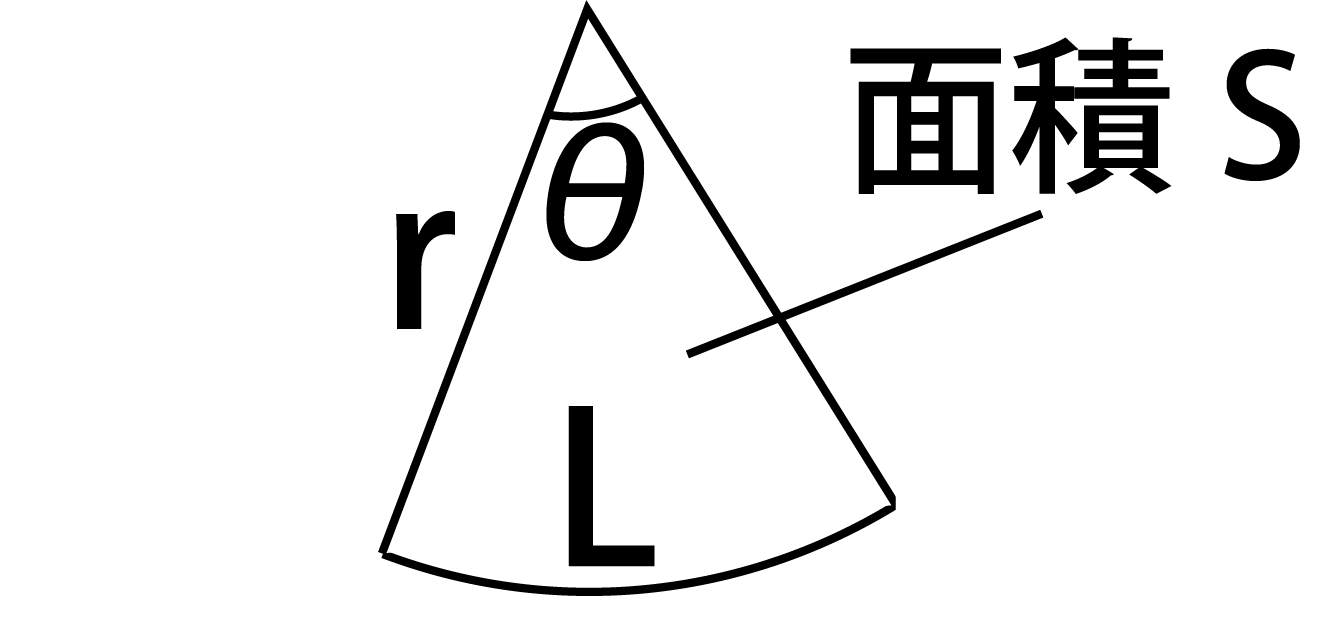
単元:おうぎ型の中心角の解き方 問題 半径9㎝、弧の長さが6n㎝のおうぎ形の中心角を求めなさい。 中学生数学特訓プラン 基礎力養成特訓プラン 推奨学年中学1年~中学3年生内容計算の基礎養成演習時間割 円すいの展開図、中心角の公式を知って5秒で解こう♪ 面積 面積 円すいの展開図の中心角を求めなさい。 円周率は314とします。 知りたがり 何に注目 すれば 「 おうぎ形の面積の求め方 」はつぎの公式であらわされるんだ。 半径をr、面積をS、円周率をπ、中心角をαとすると、 S = πr² × α / 360




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者




おうぎ形の面積の求め方 次世代型個別指導塾アチーブメント Achievement
ってことは、「 比例式から求める方法」を知っておけば公式を忘れても大丈夫 ってことになる。 念のために、 公式に頼らない「扇形の中心角の求め方」 をみていこう。 さっきの「半径4cm、弧の長さ6π cmの扇形」の中心角を求めてみるよ。 中心角はつぎの3ステップで計算できるんだ。 Step1 扇形の中心角をx°とおく まずは「扇形の中心角」を「x円の面積を求めるためには の公式にあてはめます。 (2)半径4㎝、中心角45°のおうぎ形の弧の長さと面積を求めなさい。 (2)解説&答えはこちら 答え 弧の長さ: 面積: 弧の長さを求めるためには の公式にあてはめます。 円の面積を求めるためには の公式にあてはめます。 (3)半径8㎝、中心角90°のおうぎ形の弧の長さと面積を求めなさい。エ 円やおうぎ形についての基本的な用語の意味を知り,その表し方を理解するとともに, おうぎ形の中心角と弧の長さ,中心角と面積の関係について理解する。 オ おうぎ形の弧の長さや面積を求めることが出来るようにする。




扇形の中心角の求め方 途中式をていねいに解説 面積 弧の長さから求める方法 中学数学 理科の学習まとめサイト




公式を図解 すい体の体積 円すいの表面積の求め方
扇形の面積は、同じ半径の円の面積に中心角の割合をかければ求められます。 扇形の面積の求め方 \begin{align}\text{(扇形の面積)} = \text{(円の面積)} \times \text{(中心角の割扇形の中心角の求め方 (1) 円錐(円すい)の問題ですが、立体と考えず平面で考えればただの中心角の問題です。 覚えておかなければならないのは、円すいの展開図のだいたいの形です。 円すいの展開図は「 おうぎ形 + 円 」です。 そして、大切なことは、一般に中心角 の扇形の面積は,円の面積のx/360 だから ** 中3の三平方の定理を習ってからやる問題 ** この円すいの展開図をかいたとき,側面になるおうぎ形の中心角を求めなさい。




おうぎ形 面積 弧の長さ 中心角の求め方を問題解説 数スタ




扇形の公式は暗記しない 割合という考え方を導入するだけでスラスラ解ける 中学受験ナビ
おうぎ形の面積は 半径 × 半径 × π × 中心角/360 という公式を使えば 出すことができましたね。 しかし、下の図のように 肝心の中心角がわかっていない場合 弧の長さを使って中心角を出してから} { x=80 } が答えになります。 弧 の 長 さ 半 径 中 心 角 弧 の 長 さ = 半 径 × 2 × 314 × 中 心 角 360 ∘ 中心角のわかっている、おうぎ型の 面積 を求める公式 面 積 半 径 半 径 中 心 角 面 積 = 半 径 × 半 径 × 314 × 中 心 角 360 ∘ 面積を2倍 にすると 面 積 半 径 半 径 中 心 角 面 積 ×




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者
これは、公式に当てはめるだけで答えが出てきます。 おうぎ形の中心角を求める公式は x=\displaystyle \frac { 180l } { πr } でしたね。 これに当てはめて、 x=\displaystyle \frac { 180×4π } { π×9 } よって、 \style { colorred; 半径3cmで面積が3π㎠のおうぎ形の中心角を求めます。 まずは同じ半径(3㎝)を持つ円の面積を求めます。 3×3×π=9π あとは公式に当てはめていくと 弧度法を使ったおうぎ形の弧の長さと面積 半径が r r で、中心角が θ θ のおうぎ形の弧の長さを l l とし、面積を S S とすると、次が成り立つ。 l = rθ S = 1 2r2θ = 1 2rl l




扇形の面積の出し方と特殊な場合の公式 たぬぬ塾 中学校の先生たち




標準 おうぎ形と正方形の面積 なかけんの数学ノート
扇形の面積は、「 半径が等しい扇形の面積は、中心角に比例する 」という性質を使って、円の面積 πr2 π r 2 に 中心角 360∘ 中心角 360 ∘ の 割合 をかけることで求められます。




Kelas 7 Catatan Tentang 中1 数学 範囲 Clear




おうぎ形の弧長 面積 中心角 半径 具体例で学ぶ数学




扇形の面積 弧の長さ まわりの長さの求め方 公式 小学生 中学生の勉強




3分で分かる 扇形 おうぎ形 の面積と弧の長さの求め方 公式をわかりやすく 合格サプリ




円 半円 弧 扇形 の円周 面積の求め方と公式一覧 小学生の算数 Yattoke 小 中学生の学習サイト




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ




おうぎ形の中心角の求め方 Youtube



円錐の側面であるおうぎ形の中心角を求める問題 バカでもわかる 中学数学



中学1年生数学 おうぎ型の中心角の求め方 長野地区 Itto個別指導学院 長野市の学習塾




小学校6年生の算数 数学fun 数学 小学校 算数 算数




弧の長さを使った扇 おうぎ 型の面積の公式を知っていますか




円錐の母線 半径 中心角の関係式とそれぞれの求め方 具体例で学ぶ数学




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット



おうぎ形の弧の長さと面積の求め方 小学生に教えるための解説 数学fun




扇形の中心角の求め方を教えてください Clear



中1数学 円とおうぎ形 では 円の性質とおうぎ形の面積の求め方が項目理解の重要ポイント 桜華塾 お役立ちブログ 楽天ブログ




おうぎ形面積の超簡単な求め方 合同会社エスキージャパン



おうぎ形の面積と弧の長さの求め方 バカでもわかる 中学数学




中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく



扇形の中心角の求め方を教えてください 中心角の求め方は2通りのパタ Yahoo 知恵袋




扇形の面積の求め方 公式と計算例




この周の長さが12p 12 Cm なのですが分からないので解き方を教えてください Clear




扇 おうぎ 形の面積を求める公式と弧の長さの求め方
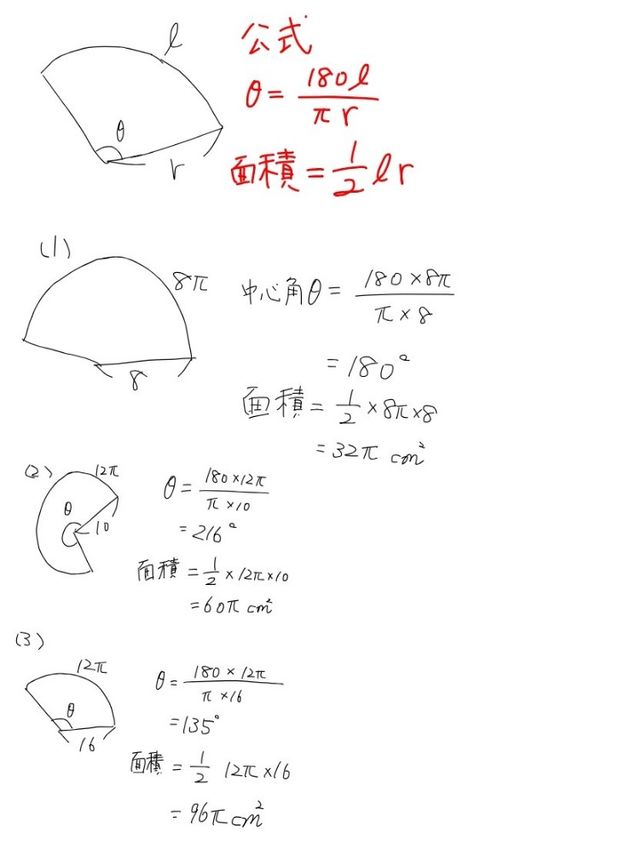



1 8cm 8cm Descubre Como Resolverlo En Qanda




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
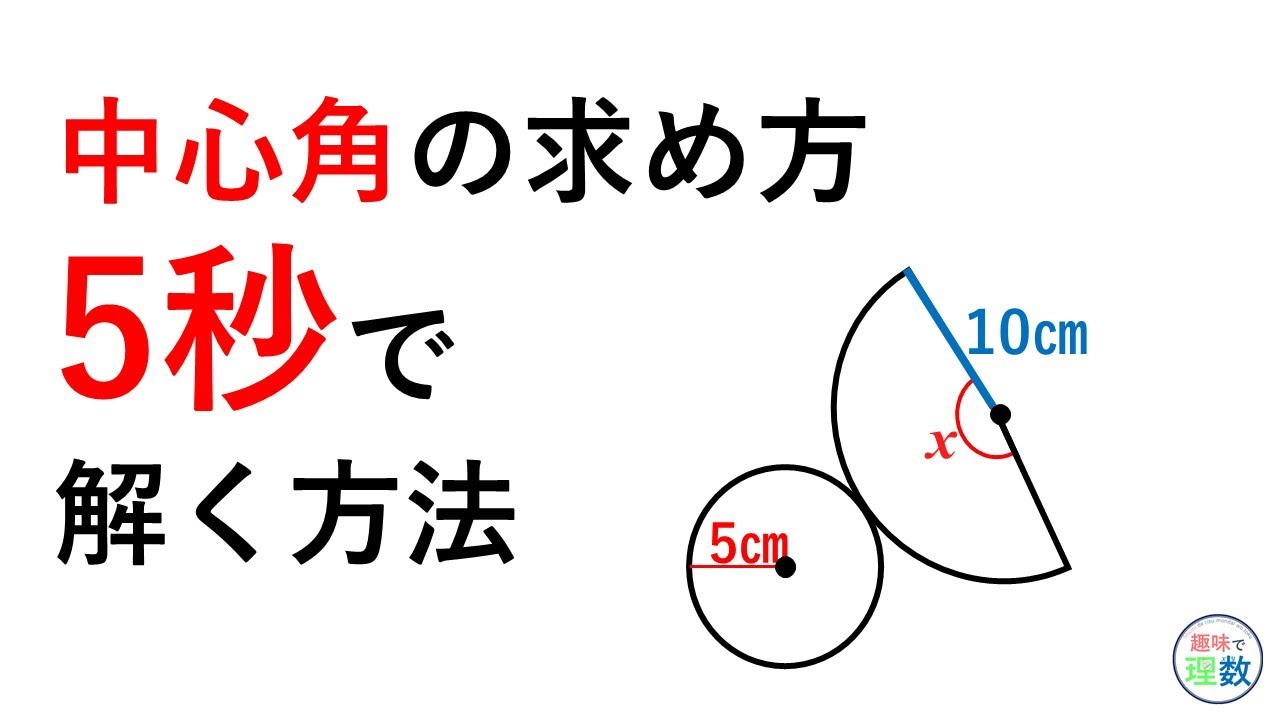



おうぎ形の中心角の求め方 Youtube




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



おうぎ形の面積の公式 算数の公式




3分で分かる 中心角の求め方ー公式とその証明 練習問題をわかりやすく 合格サプリ



3




おうぎ形の面積と弧の長さの公式 全国 中学数学ができるようになるブログ




中学数学 おうぎ形の中心角を求める問題 Youtube



扇形とは 面積 中心角 半径 弧の長さの公式と求め方 受験辞典



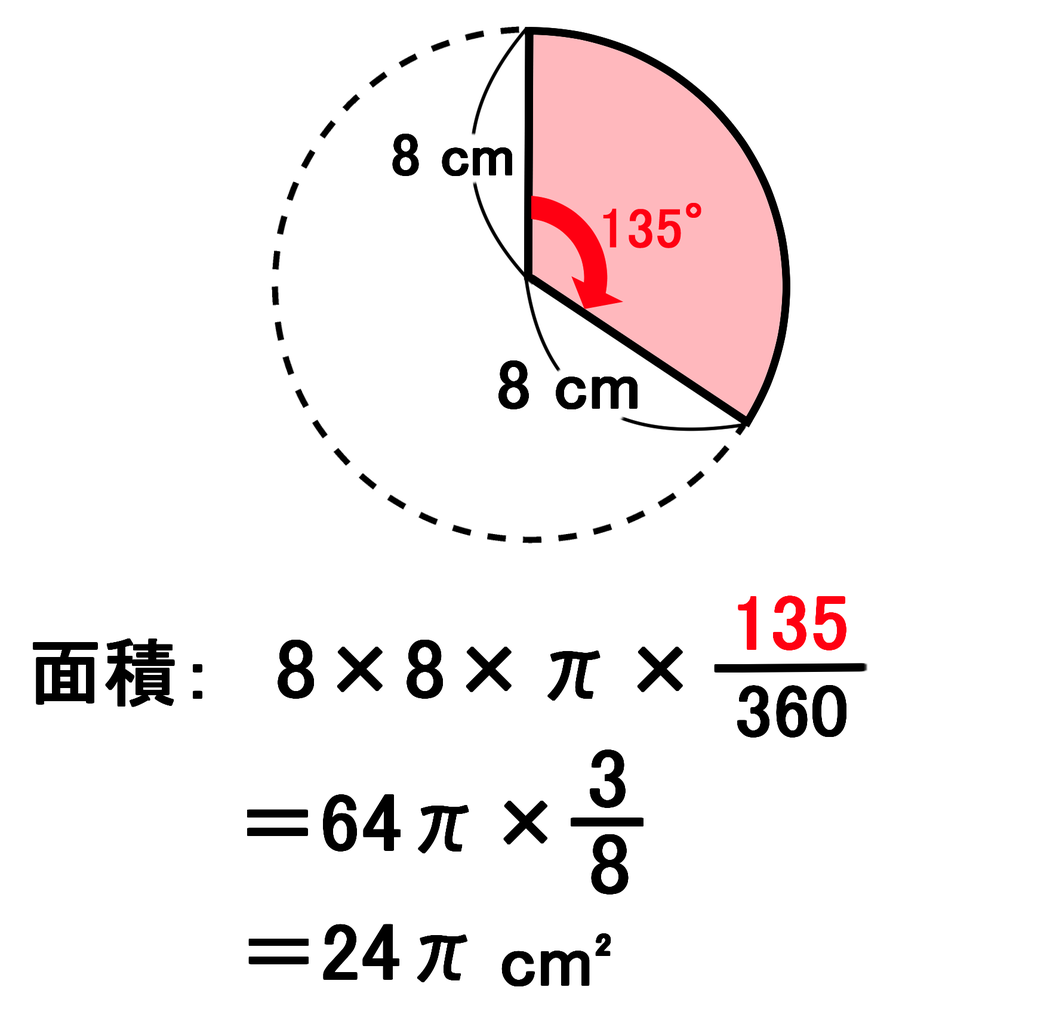
半径8cm 中心角135 のおうぎ形の弧の長さと面積を求めてくださ Yahoo 知恵袋



中心角40度 弧の長さ2pcmの扇形の面積中心角30度 弧の長さpcmの扇形 Yahoo 知恵袋




扇形の弧の長さと面積 小学 中学数学での平面図形の求め方 リョースケ大学




楽しい数学 中心角の裏ワザ 塾のおしごと



3



2




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




扇形の中心角とは 求め方って 円周や面積や弧の長さを使って計算 ノビコト




おうぎ形 半径の求め方 数学の記録




中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく
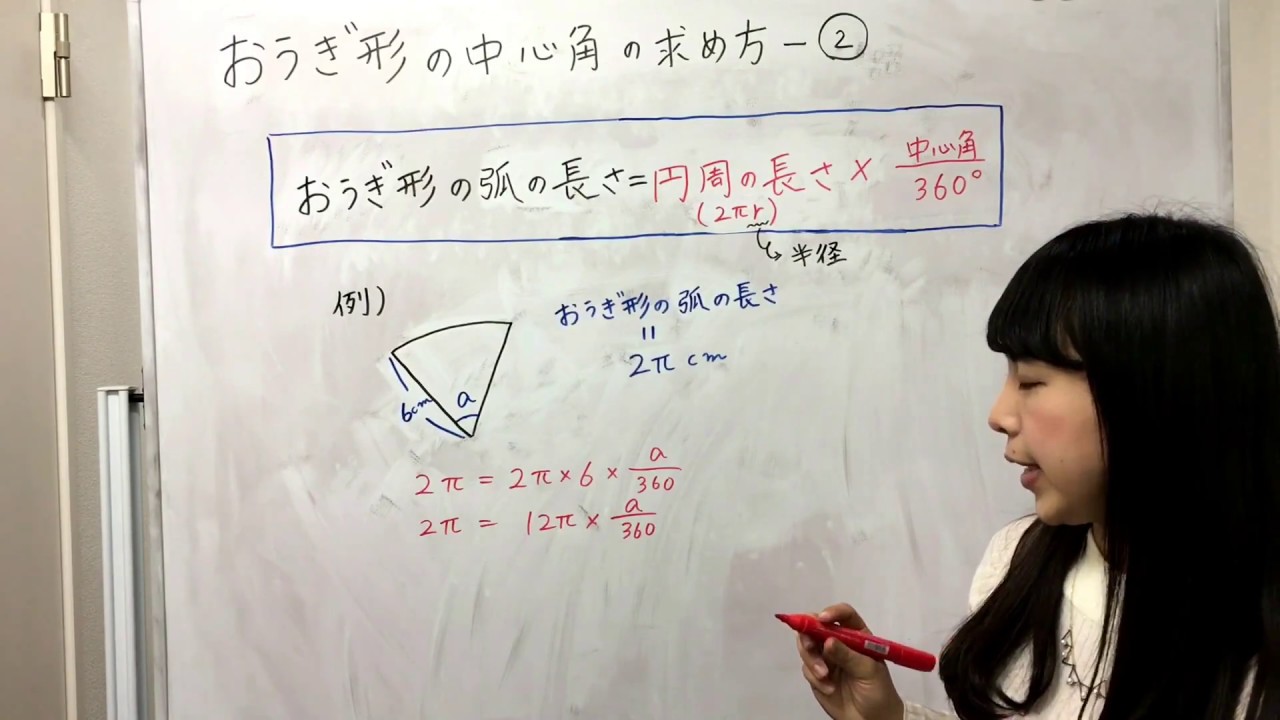



中1数学 おうぎ形の中心角の求め方 家庭教師のガンバ Youtube



1




標準 おうぎ形の弧の長さや面積 なかけんの数学ノート



おうぎ形の弧の長さと面積 が苦手でもコレなら分かる 中学1年数学 平面図系 教科書をわかりやすく通訳するサイト




扇形の弧の長さの求め方 公式と計算例




円 扇形 の面積 周や弧の長さの公式 数学fun



中学数学 平面図形 のコツ 円とおうぎ形




扇形面積公式弧長 3分で分かる 扇形 おうぎ形 の面積と弧の長さの Mtlpe




おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ




中心角の求め方が即わかる 合わせて知りたい知識とは 高校生向け受験応援メディア 受験のミカタ




平面図形 おうぎ形の中心角の求め方 中学数学 定期テスト対策サイト




おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ



扇形の面積公式が一目でわかる 丁寧な証明付き 高校生向け受験応援メディア 受験のミカタ




おうぎ形の中心角の求め方を詳しく教えてください お願いします Clear




円錐の表面積 中心角を求める問題を丁寧に解説 数スタ




中学1年生 数学 円とおうぎ形 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




円とおうぎ形の周りの長さ 面積の求め方 無料プリントあり



円錐の母線 半径 中心角の関係式とそれぞれの求め方 具体例で学ぶ数学




中1 数学 空間図形9 おうぎ形の公式 17分 Youtube




扇形の面積の求め方 小学生でも公式を簡単に使える問題です 中学や高校の数学の計算問題
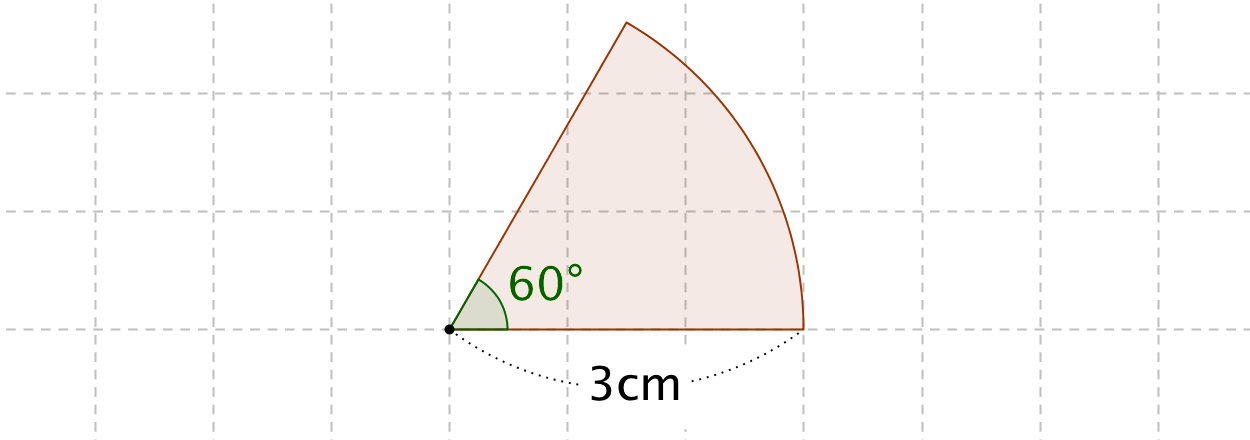



おうぎ形の面積の公式 算数の公式




中学数学 扇形の中心角の求め方3パターン ピザでわかる なぜか分かる はかせちゃんの怪しい研究室



3




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット




半径6cm 弧の長さ2pcmのおうぎがたの面積 はどーやって求めますか Clear




おうぎ形 弧の長さ 面積 中心角の求め方 学習内容解説ブログ
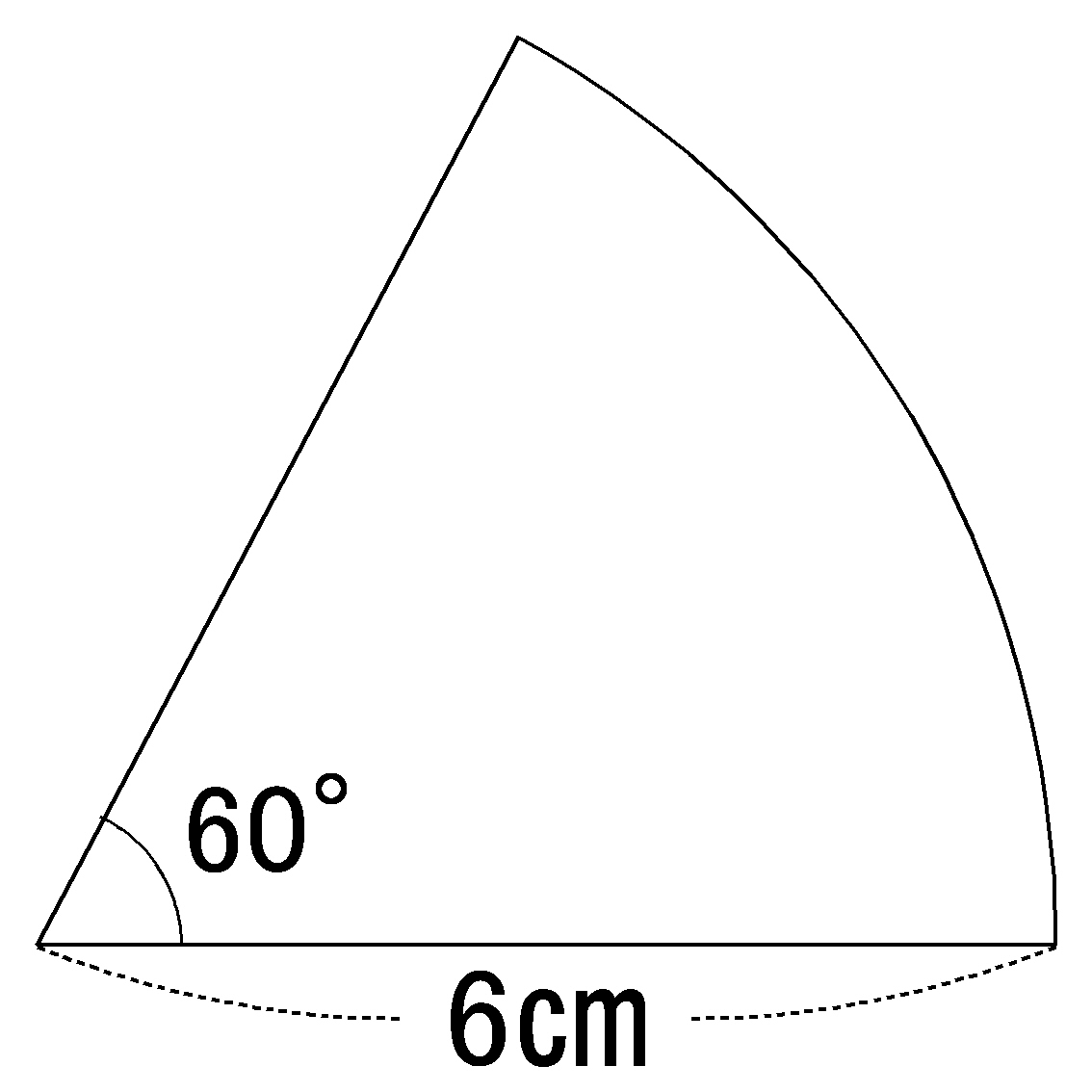



Msワードで中心角がわかっているおうぎ形 Wordで数学問題プリントを作ろう




扇形の弧の長さの公式 簡単な問題で求め方をマスターしよう 中学や高校の数学の計算問題




円錐の表面積 あんず学習塾のメモ 図表置き場




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者




中1数学 おうぎ形の公式 例題編 映像授業のtry It トライイット




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
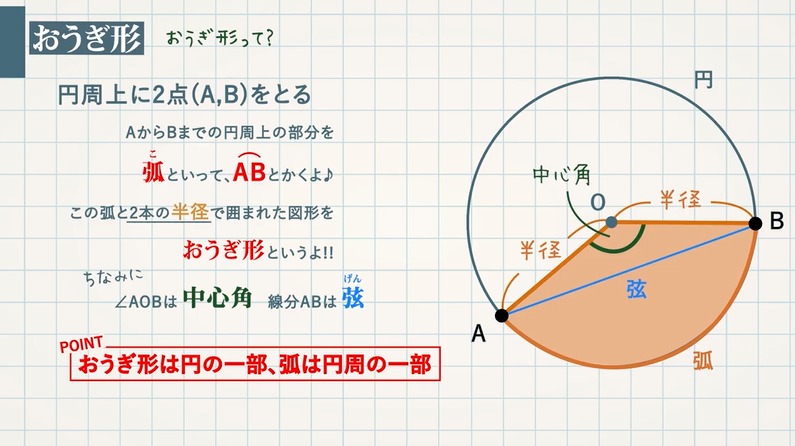



おうぎ形まとめ 弧と面積の求め方 教遊者
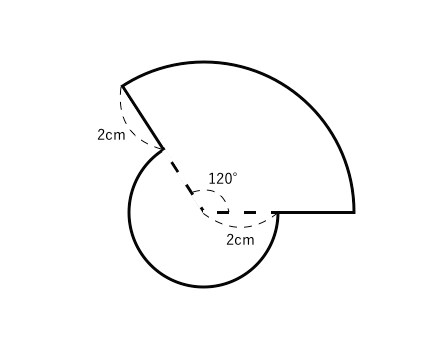



おうぎ形の問題 ちょっと応用編 苦手な数学を簡単に




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ
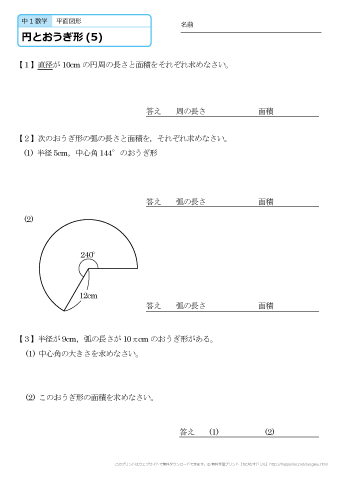



中学1年生 数学 円とおうぎ形 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中1 数学 中1 75 おうぎ形の弧と面積 基本編 Youtube




おうぎ形の弧の長さ 面積 中心角の求め方と公式 Irohabook




算数 本当に 分かる という事 おうぎ形の面積その1 エース学院




扇の弧の長さと面積の求め方 公式 中学数学 By Okボーイ マナペディア



3分で分かる 扇形 おうぎ形 の面積と弧の長さの求め方 公式をわかりやすく 合格サプリ
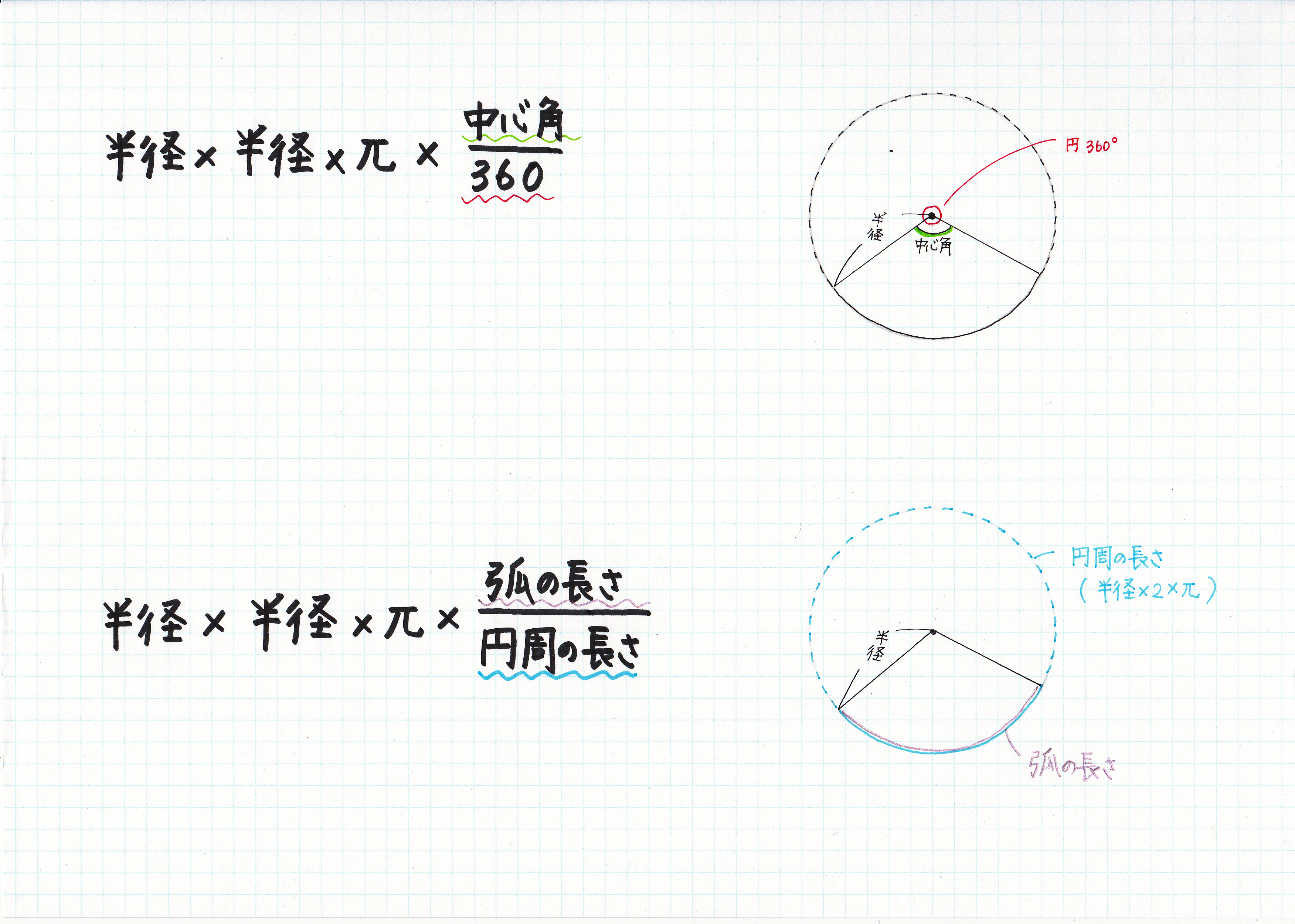



おうぎ形の面積の公式について 現役塾講師のわかりやすい中学数学の解き方
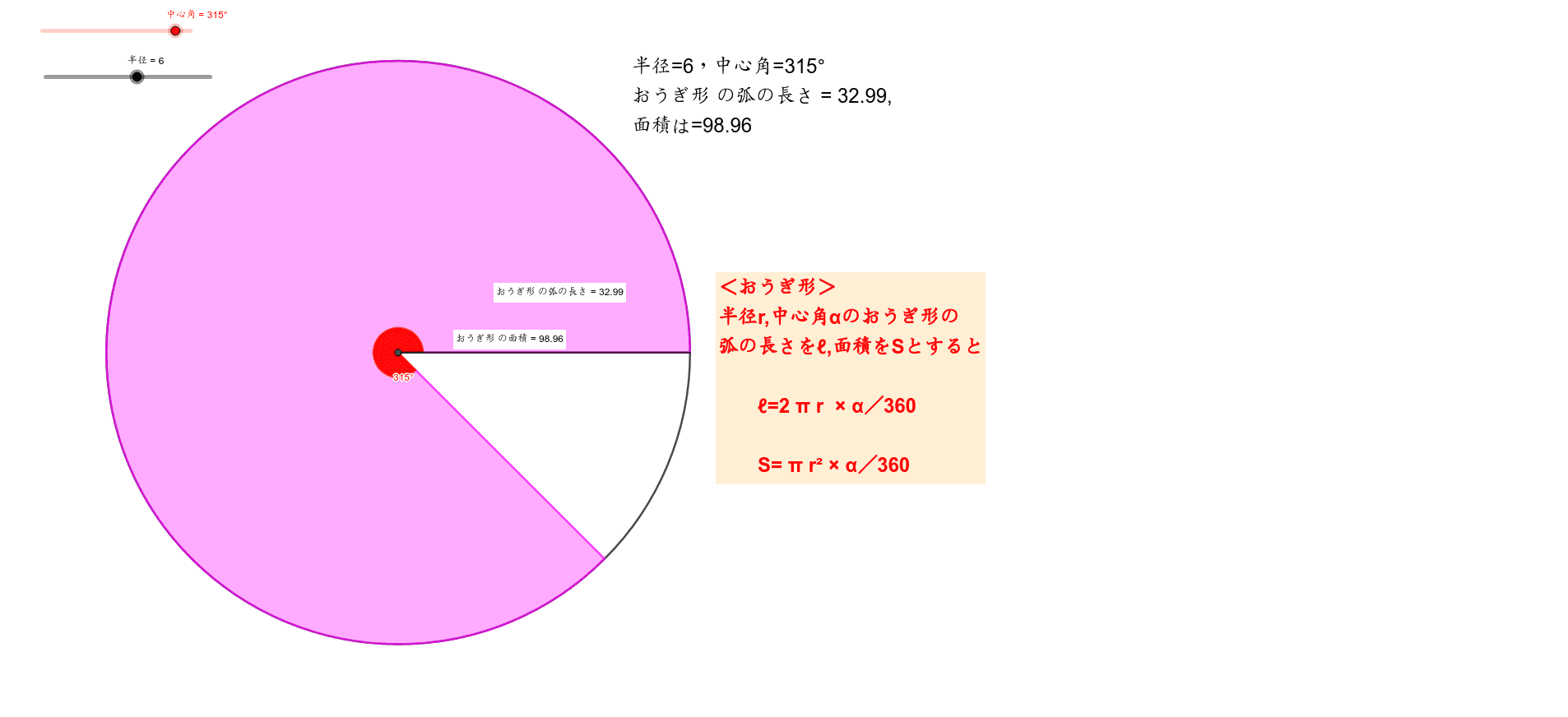



中1 おうぎ形の弧の長さや面積について考えよう Geogebra



おうぎ形の問題 パターンを知ろう 苦手な数学を簡単に



半径9cm 面積18pcm の扇形の中心角を求めなさいという問 Yahoo 知恵袋



0 件のコメント:
コメントを投稿