まず次の連立方程式を解いてみましょう。これは、二元連立一次方程式です。変数(未知 数)がx とy の二つだからです。右の列に書いたものは、方程式の係数だけを取り出し て書いたものです。 と= は省いてありますが、−3 のところは、(−3) と考えて−3問題391 複素数を表す変数x,y,z に関する次の3元連立方程式を解きなさい: 3x−6y5z=5 4x2y−z=1 7x−4y8z=2 連立方程式を構成する方程式のうちの片方が1次方程式で他方が2次方程式である ときを扱います. 例題 複素数を表す変数x,y に関する次の連立方程式を解く: ˆ 3x−2y−1=0 2y2−3x2 =3y−4x53 1 連立方程式の表現方法 連立1次方程式 (Linear Equations)は,次のような形をしている. 式 ( 7 )は行列とベクトルで書くと,式がすっきりして 考えやすくなる.書き直すと, ( 8) である.それぞれの行列とベクトルは, を表す. 通常,連立1次方程式 ( 7 )は と書き表せる.このようにすると,見通しがかなり良くなる.
25 3 連立方程式 ニスヌーピー壁紙
3連立方程式 計算
3連立方程式 計算-連立方程式の文章題のポイントは!①問題文の数に注目して、数の間の関係を見つける!②求めたいものを x , y とする。③方程式を作る。④方程方程式 1つまたは複数の変数を持つ方程式を解き,グラフを表示してこれを調べる. 一次方程式を解く 4x3=19 整方程式を解く x^2 4x 6 = 0を解く 指定の定義域で解く x^3 4x^2 6x 24 = 0を実数上で解く 方程式をパラメータについて解く




Ok423 三元一次連立方程組1 Ok423 三元一次聯立方程式主題一解聯立方程式1 可用加減消去法或代入消去法求解 2 聯立方程式的解可分成三種 1 恰有一解 2 無限多組解 3 無解 Pdf 免费下载
式にかっこが含まれる連立方程式の解き方 かっこ()が付いている式を含む連立方程式も解くことが出来ます。 一言で言うと、かっこを解いてあげれば連立方程式を解くことが出来ます。 例\begin{eqnarray}\left\{\begin{array}{l}x3y=7\\2(x2y1)y=3\end{array}\right\end{eqnarray}下記の3元連立1次方程式を考えよう。 (変数は x 1, x 2, x 3) 5x 1 3x 2 x 3 = 3 4x 1 5x 2 2x 3 = 4 x 1 3x 2 6x 3 = 6 とおき、マトリックスで表記すると、極めて簡単に A ×x = b ・・・・・ (1) となる。 EXCELのソルバーを用いて連立方程式を解く ① マトリックス( A)、 ベクトル( b) の入力 元来EXCELは行列 3元連立微分方程式 dx/dt=xyz① dy/dt=4x3y7z② dz/dt=2xy5z③ の解法 <解法1> ①×2②③をつくってみます。 右辺は、 2x2y2z4x3y7z2xy5z=0 になります。 ということは、 d2xyz/dx=0 2xyz=C₁④ になります。 よって、 yz=C₁2x を①に代入して、
連立方程式(高校入試問題) 15年~17年の公立高等学校入試問題で,連立方程式の計算問題として出題されたものを以下のA~Gの型に分類すると,右のグラフのような割合になります. すなわち,Bの型の問題が最も多く出題されており,受験勉強の時間が足りなければ,この型の問題から練習するとよい. もう少し時間に余裕があれば,他の型の問題もやって 2:連立方程式を解く方法 3:ベクトル方程式を用いる方法 入試数学コンテスト 成績上位者(Z) 1 rinno (小倉高校) 150 点 1 Kino 150 点 1 Toboggan 150 点 1 KBTIT (高校2) 150 点 1 umezo 150 点 1 takunyan (既卒) 150 点 1:外積と法線ベクトルを用いる方法 レベルは高いですが3つの中で最も計算が単純な測定された2波長赤外線カメラ3の出力値をこの関係式に代入し、2元非線形 連立方程式 を解くことにより、目標の温度及び距離を求める。 例文帳に追加 A measured output value from the twowavelength infrared camera 3 is substituted for the relational
これから連立方程式を解く問題はこの行列の形で出題されますので、元の連立方程式がどういう形なのか分かるようにしておいてくださいね! 連立方程式の解は3パターンある 連立方程式の解の出方は以下の3パターンです。 ・「 普通に解が出るパターン 」② 作った数と売れた数を、x、yを使った式で表して、連立方程式をつくりなさい。 x+y=300 ← 作った数に着目して 05x+08y=210 ← 売れた数に着目して ③ 連立方程式を解いて、作ったケーキとプリンの数を求めなさい。 -3y=-600 y=0 → ①式に代入して、x=100 x=100、y=0 は答えと例題33 今度は次の3元連立1次方程式を解いてみよう 2 35 7 0 23 5 xy z xy z xyz ìï =ïï ïí = ïï ïïî =掃き出し表 操作の内容 掃き出し表 操作の内容 拡大係数行列 x y 定数 操作 ((1)は第1 行を表す) 行基本 変形 対応する式 (消去法) ① 32 119 8 32 9(1) 8(2) xy xy= = ② 11 328



解二元一次聯立方程式 代入消去法 Live 多媒體數學觀念典online



1 4 聯立方程式 題型解析on Vimeo
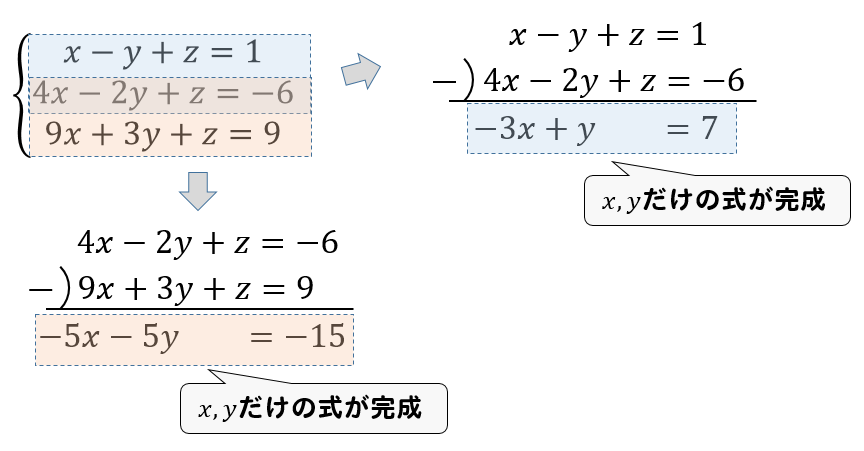
数学・算数 3元の連立方程式の空間での位置 y=2x z=y1 とします。 z=2x1 も出ます。 これを、xyz空間に描こうとすると、 各、xy, yz, zx 平面に直線が引けますが、 3 質 基礎知識とポイント 今まで解いてきた連立方程式は「x」と「y」の2つの文字だったよね? でも今回は「x」と「y」と 「z」 の3つの文字がある! これだと、普通に解けないよね? そういう時は、 文字を1つ消す んだ! ! 手順は、 消しやすい文字を見つける 「消しやすい文字を消した式」を2つ作る2章 連立方程式 年 組 番 名前 x3+4y=1 2x−y=8 x㋐ =3,y=−2は,3×3+4×(−2)=1で成り立つから,3x+4y=1の解。 2×3−(−2)=8で成り立つから,2x−y=8の解。




連立方程式 A B Cの3つ式があるときの解き方を解説 中学数学 理科の学習まとめサイト




Ch2 空間中的平面與直線2 3 三元一次聯立方程式製作老師 趙益男 基隆女中教師發行公司 龍騰文化事業股份有限公司 Ppt Download
35 連立方程式の解の集合 次 36 行列の簡約化 上 3 連立 1 次方程式 前 34 演習問題 ~ 連立 3 5 連立方程式の解の集合 注意 3 17 (連立方程式の解の集合) 連立方程式 (415) を考える. 第 1 式,第 2 式をみたす点 の集合は それぞれ 内の直線を表す. 連立方程式の解はこの 2 つの式を同時に3x2 (y3)=1 分配法則でカッコを開き、式を整理すると 3x2y=5 両辺に10をかけて小数をなくすとx2y=3 x2y=3の両辺に3をかけ、辺々引くと 3x2y = 5 ) 3x6y = 9 4y = 4 両辺を4で割るとy=1 y=1を3x2y=5に代入すると 3x2=5 3x=3 31 < 連立方程式 > 32 < spi方式 > 4 50円切手と80円切手を合わせて35枚買って、1,930円支払いました。80円切手は何枚買いましたか? 41 < 連立方程式 > 42 < spi方式 > 5 まとめ;




1 4例題3三元一次聯立方程式的無限多解 Youtube




第1章二元一次聯立方程式1 1 代入消去法一 章節內容 Ppt Download
連立方程式 2つ以上の方程式を組み合わせたものを,連立方程式という。 中学2 年で学習するのは,次のような,2 つの2 元1 次方程 式を組み合わせたものである。 (x − 4y = 8 3x 2y = −4 2 つの方程式を同時に成り立たせるx とy の値の組を,連立3 連立1次方程式 次の連立1次方程式を考える。1 a11x1 a12x2 ·· a1nxn = b1 a21x1 a22x2 ·· a2nxn = b2 am1x1 am2x2 ·· amnxn = bm (1) 行列を用い、方程式(1)は、次の行列の方程式でも表される。 a11 a12 ··a1n a21 a22 ··a2n三元連立方程式 自分の計算が不安で利用させていただきました。 思っていたより間違ってたので使ってよかったです。 4元にも対応してくれたら大変有難いです。 世界の経緯度観測所のデータ(3か所)から、形状軸からの極 (瞬間自転軸)のズレの計算に




4 2 3三元一次聯立方程式



三元一次聯立方程式 由未知數討論方程組的解 Youtube
2年 連立方程式7/11 教p4445( )年( )組( )名前 a=b=c の形の方程式は,次の3つのいずれかの形の連立方程式に ・ 連立方程式を解くには、既習である文字1つの方程式を導けばよいことに気付くことがで きる。 ・ 加減法による連立方程式の解き方(233連立 1 次方程式の基本変形 定義 38(連立 1 次方程式の基本変形) 連立 1 次方程式に対する次のの操作を連立 1 次方程式の基本変形と呼ぶ. (1) 一つの式を 倍する. (2) 二つの式を入れ替える. (3) 一つの式を 倍して別の行に加える. 連立 1 次方程式に基本変形をして得られた方程式と元の方程式とは等価な方程式である. 連立方程式について教えてください。 見ていただきありがとうございます。連立方程式の解き方が分かりません。解き方と答え教えていただきたいです。 連立方程式 ・3x5y=ー5x3yー26=3 ・4xー3y=2xyー6=2 ・2xy=5x2y=1 ・5x2y=5x6y=14 です。すみませんが教えて




2 Y 3 Y 4 Cheap Online



Http Math1 Ck Tp Edu Tw E6 9e 97 E4 Bf A1 E5 Ae E5 Ad B8 E8 A1 93 E7 A0 94 E7 B6 E4 B8 8a E8 B2 E8 Ac 9b E7 Be 99 E8 B2 E7 B6 B1 E7 Ac Ac E5 9b 9b E5 86 8a 2 3 E4 B8 E5 85 E4 B8 80 E6 Ac A1 E8 81 Af E7 Ab 8b E6 96 B9 E7 A8 8b E7 B5 84 16 Pdf
連立方程式の解を求めるための具体的な方法として、加減法と代入法の二つの方法がある。 連立を組んでいる全ての方程式が受け入れられるものが連立方程式の解になる。 一部の方程式を満たすだけでは連立方程式の解とはいえない。 menu 検索 最近の投稿 期間限定配布!「電験3種教3.連立1 次方程式の解法 4.解の分類と図形 5.おわりに 1.平面上の直線 xy平面上の直線の式を復習しておく. (a) 定点を通ってベクトルnに垂直な直線 平面上で定点P0 とベクトルnが与えられたとする (図11).P0 を通ってn に垂直な直線g の式は以下 のようにして決まる.まず,原点をOとしExcelを用いた連立方程式の解法 このページでは,Excel関数を使って連立方程式を解く手順について解説する. 手順 連立方程式を行列で表現し,行列Aと行列Cの係数をExcelシートに入力する. 解が1通り存在するのか確認する.(解が1通り存在することがわかっていれば省略可.) 係数行列Aの



三元一次連立方程式 Geogebra



1 3 2 1 4 2 2 15r
⑴ 2元1次方程式3x+4y=1の解 ⑶ 連立方程式 の解 ㋐ x =3, y =−2 x ㋑ =−5, y =44x−3y=21 (2) 「連立方程式の解」とは,左の例 (A) などにおいて2つの方程式を 両方とも満たす x , y の値のことです. 連立方程式の解を求めるには,まず,未知数が1つだけ(たとえば x だけ)の方程式を作って,解くことを考えます. x だけの方程式なら解けるからです. このように,連立方程式を解くには「未知数を1個にする」ことが鍵です.次の流れ図を3 2) 2 次の連立方程式が同じ解をもつという。 (1)同じ解を求めなさい。 (2) a, b の値を求めなさい。 { −4 =25① 2 −y=8 ② {2 8 =−14③ −3 2y=−13 ④ 同じ解をもつので,その解は②④の解 そこで,②④を連立方程式で解く。 x=3 を②に代入して,6-y=8 y=-2 x=3, y=2を①③に代入して




連立方程式 A B Cの3つ式があるときの解き方を解説 中学数学 理科の学習まとめサイト




國二junior High数学的中2 連立方程式 連立方程式 筆記 Clear
まず,3元の連立方程式で連立方程式を解く目標を 説明します.x1,x2,x3を未知数とする連立方程式を 考えます. a11x1a12x2a13x3 = α1 a21x1a22x2a23x3 = α2 a31x1a32x2a33x3 = α3 このとき,以下の3つ操作を用いて,上の連立方程 式に同値な変形を施していきます. •ある式を何倍かして他の式に加える第3回連立方程式の一般解 本日の講義の目標 目標3 1 連立方程式の解をパラメータを用いて表す方法について理解する 2 連立方程式に解が存在しない場合の扱いについて理解する 23/98たとえば、連立方程式x y = 4、2x3y = 3を解くには、最初の方程式で変数xを分離してx = 4yを取得し、このyの値を2番目の方程式に代入して2を取得します(4y)3y =3。この方程式は、5y = 5またはy = 1に簡略化されます。この値を2番目の方程式に代入して、xの値を見つけます:x 1 = 4またはx = 3




4 2 3三元一次聯立方程式




三元連立方程式 1 中2数学 Youtube
(3) 連立方程式 x−y =2 x−y =1 を解きなさい. 答以下のように解けばよい. Solve{xy==2,xy==1},{x,y} 3 このとき out5 {} と出力される.{} は解が存在しないということを意味する. 2.関数NSolve,関数FindRoot?NSolve,?FindRoot タイプし,実行するとこの使い方の説明が表示され連立方程式(加減法3) 連立方程式を解け 3x4y=6 4x3y=17 5x8y=23 8x3y=27 2x7y=6 5x6y=x3y=15 9x7y=48 11x3y=37 6x5y=60 9x7y=297x3y=31 4x5y=18 6x7y=265x6y=72 7x8y=9812x13y=17 16x15y=11 9x14y=16 6x5y=118x15y=10x21y=34 24x25y=27 16x27y=4912 3 連立一次方程式Ax = 0 の基本解 ここでは、定数項ベクトルが零ベクトルであるような連立一次方程式Ax = 0 の実数解全体 のなす集合について考える。 まず、連立一次方程式Ax = 0 はx = 0 を必ず解に持つことに注意しよう。この解を自明な 解という。 { 90 {線形代数1・第12 回(21 年6 月29 日




三元一次連立方程式を一発で解く方法 Geogebra




Intro Linear Note
3 行列と連立方程式 行列は線形代数で用いられる概念です。 また、ベクトルは行列の特別な場合です。 なお、連立方程式や固有値は、さまざまな分野で利用されます。 ベクトルx をリストとして定義する。 : 空リスト 解が存在しない。 (%o2) 3,103 2 ガウス・ジョルダン法のC言語の関数 ピボット選択は行わないで、逆行列も求めないのガウス・ジョルダン法で連立方程式を計 算するプログラムを示す。このプログラムの動作は、次の通りである。 仮引数「n」は、解くべき連立方程式の未知数の数で連立方程式を解け 3 (2xy)=3x7y23 2 (3x7y)7x=27 7 (x3y)=2 (6x5y)25 11y6 (3x2y)=22 x=5y7 3 (2xy)=4 (x3)24 3 (3xy)=5 (2x3y)15 y=3x5 4x3y=2 (7xy)10 7 (6x1)3 (8y5)=4 2 (5x2y)=3 (4xy)11 4x7y=13 2 (4x3y)=7 (xy)8 3 (x1)=2 (2y9)6 5 (x4y)=2 (2x6y7)13 4x11y=5 (2x3y2)4 5 (2xy7)=2x3y9 7xy5=3 (3x4y14)4 8x=2



25 3 連立方程式 ニスヌーピー壁紙



克拉瑪公式解三元一次方程組 紀算補習班 數學補習班 三重 文理補習班 國小數學 國中數學 隨意窩xuite日誌




高校数学 3元連立1次方程式 一般型と循環型 受験の月



連立方程式 行列計算for Android Apk Download




二元一次聯立方程式的圖形 劉繼文 新泰國中 Shareclass




Ch2 空間中的平面與直線2 3 三元一次聯立方程式製作老師 趙益男 基隆女中教師發行公司 龍騰文化事業股份有限公司 Ppt Download



Http Math1 Ck Tp Edu Tw E6 9e 97 E4 Bf A1 E5 Ae E5 Ad B8 E8 A1 93 E7 A0 94 E7 B6 E4 B8 8a E8 B2 E8 Ac 9b E7 Be 99 E8 B2 E7 B6 B1 E7 Ac Ac E5 9b 9b E5 86 8a 2 3 E4 B8 E5 85 E4 B8 80 E6 Ac A1 E8 81 Af E7 Ab 8b E6 96 B9 E7 A8 8b E7 B5 84 16 Pdf




建宏國中e把罩數學 3 二元一次聯立方程式



三元一次方程式求連比 紀算補習班 數學補習班 三重 文理補習班 國小數學 國中數學 隨意窩xuite日誌




三元1次方程式の計算法 Youtube




連立方程式の解き方とは 代入法か加減法で計算しよう 分数の問題や文章題アリ 遊ぶ数学




例題 代入消去法 Y Ax B 數學 均一教育平台




連立方程式 3つの文字 式の問題を計算する方法は 数スタ




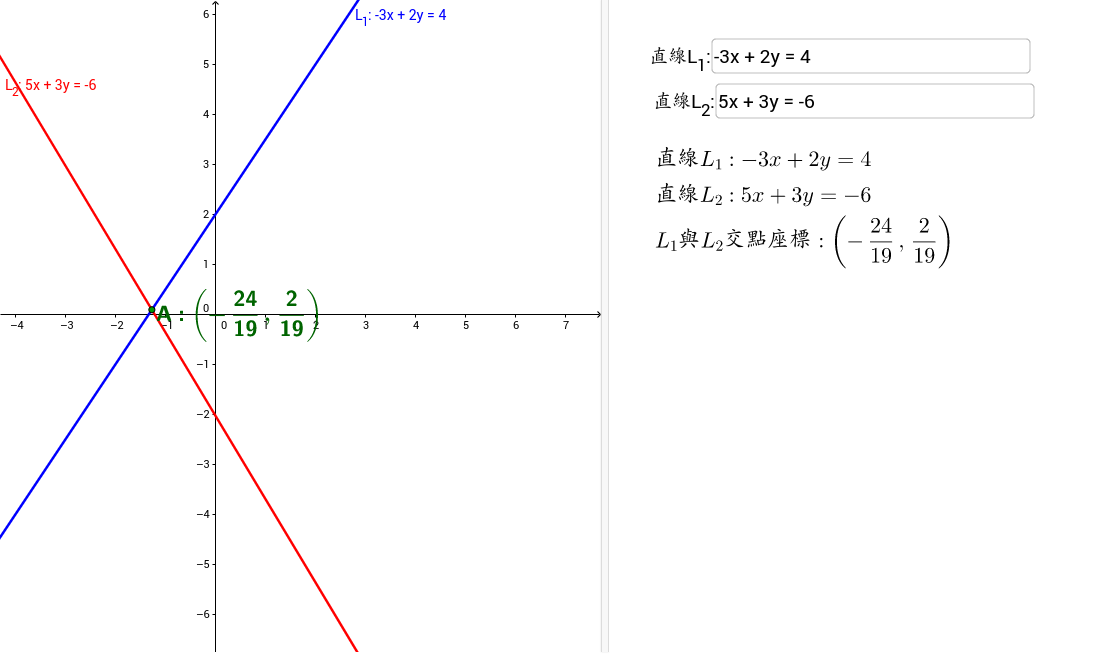
像上面兩個二元一次方程式x Y 70 和x 2y 115 雖然各自有解 但是當聯立在一起時 我們要找的就是同時能讓兩個方程式等號成立的x Y 值 此時的x 與y 就是這兩個方程式的一組共同解 也就是聯立方程式的解 但是 要如何求出二元一次聯立方程式的解呢 讓我們先以二



1




1 4 聯立方程式 題型解析on Vimeo




Ch2 空間中的平面與直線2 3 三元一次聯立方程式製作老師 趙益男 基隆女中教師發行公司 龍騰文化事業股份有限公司 Ppt Download




中2数学 連立方程式の解き方と定期テスト予想問題 Pikuu




連立3元1次方程式 まなびの学園



測評網 國一下 數學第一次段考 複習錦囊




ある連立3元3次方程式を解いてみよう 身勝手な主張




Rank Of Matrices And Homogeneous Linear Equations




中2数学 a b cの連立方程式 練習編 映像授業のtry It トライイット




連立方程式計算安卓下载 安卓版apk 免费下载




Ok423 三元一次連立方程組1 Ok423 三元一次聯立方程式主題一解聯立方程式1 可用加減消去法或代入消去法求解 2 聯立方程式的解可分成三種 1 恰有一解 2 無限多組解 3 無解 Pdf 免费下载



Q Tbn And9gctivnh0ytvm5iq2nnhaeu2fa7uykcwky0 V7mocdeysfgddbodx Usqp Cau




B4 2 3 三元一次方程組的加減消去法 理論 與範例1 用加減消去法解三元一次方程組 Youtube




Ok423 三元一次連立方程組1 Ok423 三元一次聯立方程式主題一解聯立方程式1 可用加減消去法或代入消去法求解 2 聯立方程式的解可分成三種 1 恰有一解 2 無限多組解 3 無解 Pdf 免费下载




連立方程式 1 代入法と加減法 バカでもわかる 中学数学




Intro Linear Note



Http Www Camdemy Com Sysdata Course 19 19 Doc 2fa6765cdb913af3 Pdf Pdf



Http Math1 Ck Tp Edu Tw E6 9e 97 E4 Bf A1 E5 Ae E5 Ad B8 E8 A1 93 E7 A0 94 E7 B6 E4 B8 8a E8 B2 E8 Ac 9b E7 Be 99 E8 B2 E7 B6 B1 E7 Ac Ac E5 9b 9b E5 86 8a 2 3 E4 B8 E5 85 E4 B8 80 E6 Ac A1 E8 81 Af E7 Ab 8b E6 96 B9 E7 A8 8b E7 B5 84 16 Pdf




三元一次聯立方程式 利用克拉瑪公式判斷三平面關係之一 Youtube




怎麼知道的 紅線 Clear



連立方程式3つあるときの計算方法は 例題を使って解き方を解説 方程式の解き方まとめサイト




高校数学 3つの解から3次方程式の作成 3変数対称式の連立方程式 受験の月




隨筆誌 二下2 3三元一次聯立方程式比例式解題想法




未定係数を含む3元連立方程式の解 数学解説ブログ つくば市の 数学 算数 物理に強い プロ家庭教師 長通幸大 発信



大家來解謎 解二元一次聯立方程式 導入活動 環遊數界




Xyz 3つの式の連立方程式の解き方がわかる4ステップ Qikeru 学びを楽しくわかりやすく




Rimg0010 連立方程式を解くウィルバーマシン Masakazu Takahashi Flickr



連立方程式3つあるときの計算方法は 例題を使って解き方を解説 方程式の解き方まとめサイト
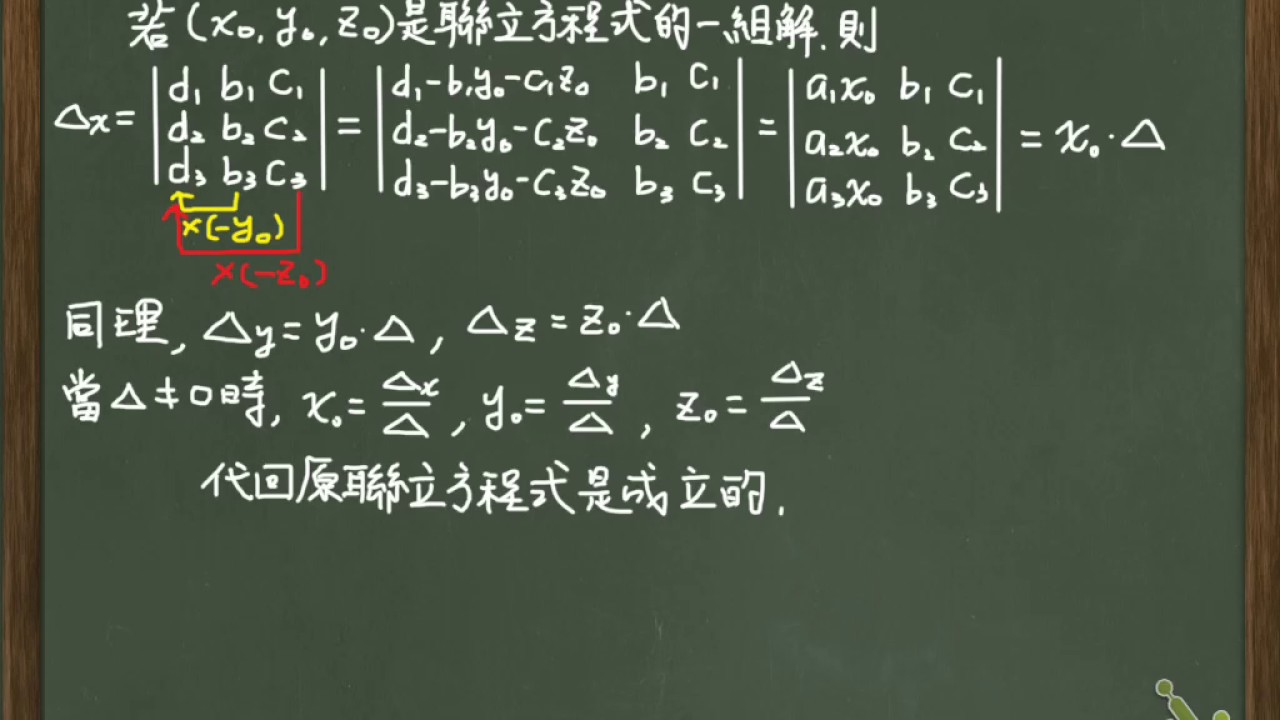



40 三元一次聯立方程式的公式解 克拉瑪公式的說明 Youtube




單元一二元一次聯立方程式討論一二元一次方程式 林晟數學online




大家來解謎 解二元一次聯立方程式 導入活動 環遊數界




均一影片 例題 解二元一次聯立方程式 綜合應用3 學習單 Shareclass



二元一次聯立方程式圖解 Geogebra




方程式計數機連立一次方程式の計算機 Cpdpg



名師課輔網 係數對稱的聯立方程式



3 1進階01指數聯立方程式 數學 均一教育平台




25 3 連立方程式 ニスヌーピー壁紙



1




解二元一次聯立方程式綜合應用3 Youtube




Xyz 3つの式の連立方程式の解き方がわかる4ステップ Qikeru 学びを楽しくわかりやすく




連立方程式の解き方とは 代入法か加減法で計算しよう 分数の問題や文章題アリ 遊ぶ数学




中2数学 a b cの連立方程式 練習編 映像授業のtry It トライイット



三元一次聯立方程式 解三元一次方程組 Youtube



25 3 連立方程式 ニスヌーピー壁紙




連立3元1次方程式 身勝手な主張
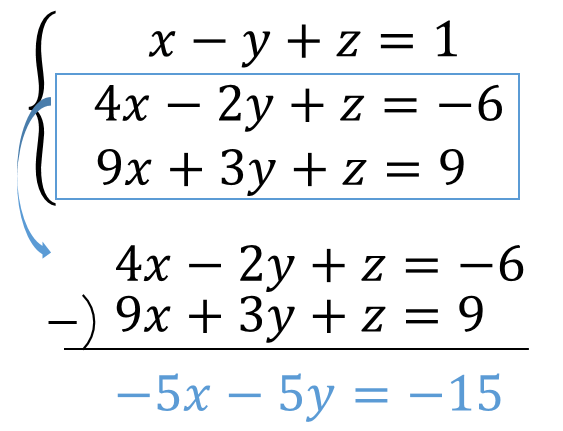



連立方程式 3つの文字 式の問題を計算する方法は 数スタ




25 3 連立方程式 ニスヌーピー壁紙



1




例題 連立3元1次方程式の解き方 Youtube




連立方程式で3つの式がある時の解き方が誰でも分かる 高校生向け受験応援メディア 受験のミカタ




隨筆誌 二下2 3三元一次聯立方程式 克拉瑪法則證明




用matlab 0 Cript解聯立方程式 Labview Labview360論壇




25 3 連立方程式 ニスヌーピー壁紙




3分で分かる 式が3つの連立方程式の解き方をわかりやすく解説 合格サプリ



6 3 聯立方程式聯立方程式求行列式6 8 2 15 5 3 4 1 之值 求行列式15 10 15 15 0 6 2 6 4




summer05 Png
.png)



2元一次方程式題目初中數學 二元一次方程式 例題2 Gquhm




ある連立3元3次方程式を解いてみよう 身勝手な主張




方程式計數機連立一次方程式の計算機 Cpdpg




連立方程式 3つの文字 式の問題を計算する方法は 数スタ




例題 解二元一次聯立方程式 綜合應用1 數學 均一教育平台



3 Y 15 Cheap Online




トップ100連立方程式公式 最高のカラーリングのアイデア




Ch2 空間中的平面與直線2 3 三元一次聯立方程式製作老師 趙益男 基隆女中教師發行公司 龍騰文化事業股份有限公司 Ppt Download




連立方程式で3つの式がある時の解き方が誰でも分かる 高校生向け受験応援メディア 受験のミカタ



第1章 連立方程式




連立3元一次方程式でこのように詰んでしまいます Clear



三元一次方程式excel 40 三元一次聯立方程式的公式解 克拉瑪公式的說明 Mtlpe




連立方程式で3つの式のある3元1次方程式とは 3元連立方程式の解き方をわかりやすく解説 Himokuri




Lookaside Fbsbx Com Lookaside Crawler Media Me



連立方程式とは 代入法と加減法 計算問題や文章題の解き方 受験辞典




4 2 3三元一次聯立方程式



0 件のコメント:
コメントを投稿